Question

已知集合A={x|x²＋4x=0，x∈R}，B={x|x²＋2(a＋1)x＋a²－1=0，x∈R}，若A∪B=A，求实数a的取值范围．

Answer 1

解析：本题主要考查集合的运算和包含关系，解题过程中运用了分类讨论思想，分类时易漏掉B为空集的情况，应引起重视．

解：因为A={x|x(x＋4)=0}={0，－4}，B={x|x²＋2(a＋1)x＋a²－1=0，x∈R}，且BA，所以B=，或{0}，或{－4}，或{0，－4}．?

（1）当B=时，方程x²＋2(a＋1)x＋a²－1=0无实根，即Δ＜0，解得a＜－1．?

（2）当B={0}时，方程x²＋2(a＋1)x＋a²－1=0有唯一根0，所以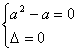

解得a=－1．?

（3）当B={－4}时，方程x²＋2(a＋1)x＋a²－1=0有唯一根－4，所以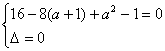.解得a无解．?

（4）当B={0，－4}时，方程x²＋2(a＋1)x＋a²－1=0有两根0，－4，所以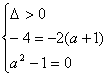.解之，得a=1．

综合（1）（2）（3）（4），可知a≤－1或a=1．