题目内容
已知集合A={x|y=x2,x∈Z},B={y|y=x2,x∈Z},则A与B的关系是( )
分析:由已知中集合A={x|y=x2,x∈Z},B={y|y=x2,x∈Z},我们可得集合A表示一个整数集,而集合B表示一个完全平方数,然后可分析集合A与B的关系.
解答:解:∵当x∈A={x|y=x2,x∈Z}时,
x为一个整数,但不一定是完全平方数,
故x∈A⇒x∈B为假命题
而当x∈B={y|y=x2,x∈Z}时,
x是一个整数的完全平方数一定是整数,
故x∈B⇒x∈A为真命题
故集合B是集合A的真子集
故B?A
故选C
x为一个整数,但不一定是完全平方数,
故x∈A⇒x∈B为假命题
而当x∈B={y|y=x2,x∈Z}时,
x是一个整数的完全平方数一定是整数,
故x∈B⇒x∈A为真命题
故集合B是集合A的真子集
故B?A
故选C
点评:本题考查的知识点是集合的包含关系判断及其应用,其中正确理解集合A与集合B的含义是解答本题的关键.

练习册系列答案
相关题目
已知集合A={x|y=
,x∈Z},B={y|y=x2+1,x∈A},则A∩B为( )
| 1-x2 |
| A、∅ | B、{1} |
| C、[0,+∞) | D、{(0,1)} |
已知集合A={x|y=
},B={y|y=3x,x>0},定义A*B为图中阴影部分的集合,则A*B( )
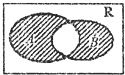
| 2x-x2 |

| A、{x|0<x<2} |
| B、{x|1<x≤2} |
| C、{x|0≤x≤1或x≥2} |
| D、{x|0≤x≤1或x>2} |
已知集合A={x|y=lg(x+3)},B={x|x≥2},则下列结论正确的是( )
| A、-3∈A | B、3∉B | C、A∪B=B | D、A∩B=B |
已知集合A={x|y=lgx},B={x|x2+x-2≤0},则A∩B=( )
| A、[-1,0) | B、(0,1] | C、[0,1] | D、[-2,1] |