题目内容
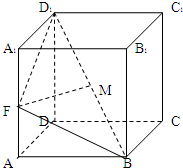 如图,已知棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1,F为棱AA1的中点,M为线段BD1的中点,
如图,已知棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1,F为棱AA1的中点,M为线段BD1的中点,(1)求证:MF∥面ABCD;
(2)求证:MF⊥面BDD1B1.
分析:(1)连接AC、BD交于点O,再连接MO,证明OM∥AF且OM=AF,MF∥OA,然后证明MF∥面ABCD;
(2)通过底面是菱形,证明AC⊥面BDD1B1,然后证明MF⊥面BDD1B1.
(2)通过底面是菱形,证明AC⊥面BDD1B1,然后证明MF⊥面BDD1B1.
解答: (1)证明:连接AC、BD交于点O,再连接MO,
(1)证明:连接AC、BD交于点O,再连接MO,
∴OM∥
A1A且OM=
A1A,
又∵AF=
A1A,
∴OM∥AF且OM=AF,
∴四边形MOAF是平行四边形,
∴MF∥OA,
又∵OA?面ABCD,MF?面ABCD,
∴MF∥面ABCD;
(2)证明:∵底面是菱形,
∴AC⊥BD
又∵B1B⊥面ABCD,AC?面ABCD
∴AC⊥B1B,BD∩B1B=B,
∴AC⊥面BDD1B1
又∵MF∥AC,
∴MF⊥面BDD1B1.
 (1)证明:连接AC、BD交于点O,再连接MO,
(1)证明:连接AC、BD交于点O,再连接MO,∴OM∥
| 1 |
| 2 |
| 1 |
| 2 |
又∵AF=
| 1 |
| 2 |
∴OM∥AF且OM=AF,
∴四边形MOAF是平行四边形,
∴MF∥OA,
又∵OA?面ABCD,MF?面ABCD,
∴MF∥面ABCD;
(2)证明:∵底面是菱形,
∴AC⊥BD
又∵B1B⊥面ABCD,AC?面ABCD
∴AC⊥B1B,BD∩B1B=B,
∴AC⊥面BDD1B1
又∵MF∥AC,
∴MF⊥面BDD1B1.
点评:本题考查空间想象能力,直线与平面平行的证明方法,判定定理的应用.

练习册系列答案
相关题目
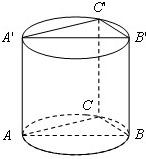 如图,直三棱柱ABC-A′B′C′内接于高为
如图,直三棱柱ABC-A′B′C′内接于高为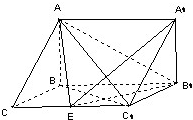 如图,在三棱柱△ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=2,∠BCC1=
如图,在三棱柱△ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=2,∠BCC1= 如图,在三棱柱ABC-A1B1C中,已知AC⊥BC,AB⊥BB1,CD⊥平面AA B1B,AC=BC=2.
如图,在三棱柱ABC-A1B1C中,已知AC⊥BC,AB⊥BB1,CD⊥平面AA B1B,AC=BC=2. 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A,ACC1A1均为正方形,∠BAC=90°,AB=2,点D1是棱B1C1的中点.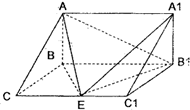 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,E为棱CC1的中点,已知AB=
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,E为棱CC1的中点,已知AB=