题目内容
 如图,平面上有一长12cm,宽10cm的矩形ABCD内有一半径为1cm的圆O(圆心O在矩形对角线的交点处).把一枚半径1cm的硬币任意掷在矩形内(硬币圆心落在矩形内),则硬币不与圆O相碰的概率为( )
如图,平面上有一长12cm,宽10cm的矩形ABCD内有一半径为1cm的圆O(圆心O在矩形对角线的交点处).把一枚半径1cm的硬币任意掷在矩形内(硬币圆心落在矩形内),则硬币不与圆O相碰的概率为( )分析:硬币要落在矩形内,硬币圆心应落在长12cm,宽10cm的矩形,硬币与小圆无公共点,硬币圆心距离小圆圆心要大于2,先求出硬币落在矩形内的面积,然后再求解硬币落下后与小圆没交点的区域的面积,代入几何概型的概率的计算公式进行求解.
解答:解:记“硬币不与圆O相碰”为事件A
硬币要落在矩形内,硬币圆心应落在长12cm,宽10cm的矩形,其面积为120cm2
无公共点也就意味着,硬币的圆心与圆心相距超过2cm
以圆心O为圆心,作一个半径2cm的圆,硬币的圆心在此圆外面,则硬币与半径为1cm的小圆无公共点
所以有公共点的概率为
=
则无公共点的概率为P(A)=1-
故选C

硬币要落在矩形内,硬币圆心应落在长12cm,宽10cm的矩形,其面积为120cm2
无公共点也就意味着,硬币的圆心与圆心相距超过2cm
以圆心O为圆心,作一个半径2cm的圆,硬币的圆心在此圆外面,则硬币与半径为1cm的小圆无公共点
所以有公共点的概率为
| 4π |
| 120 |
| π |
| 30 |
则无公共点的概率为P(A)=1-
| π |
| 30 |
故选C
点评:本题主要考查了几何概率的计算公式的应用,解题的关键是确定满足条件的图象的面积属于基础题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
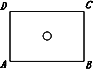
 如图,平面上有一长12cm,宽10cm的矩形ABCD内有一半径为1cm的圆O(圆心O在矩形对角线的交点处).把一枚半径1cm的硬币任意掷在矩形内(硬币圆心落在矩形内),则硬币不与圆O相碰的概率为
如图,平面上有一长12cm,宽10cm的矩形ABCD内有一半径为1cm的圆O(圆心O在矩形对角线的交点处).把一枚半径1cm的硬币任意掷在矩形内(硬币圆心落在矩形内),则硬币不与圆O相碰的概率为












