题目内容
（不等式选讲选做题）已知a，b，c∈R+，且a+b+c=1，则
+
+
的最大值为______．
| 3a+1 |
| 3b+1 |
| 3c+1 |
根据柯西不等式，可得
（
+
+
）2
=（1?
+1?
+1?
）2
≤（12+12+12）[（
）2+（
）2+（
）2]=3[3（a+b+c）+3]=18
当且仅当
=
=
），
即a=b=c=
时，（
+
+
）2的最大值为18
因此
+
+
的最大值为 3
．
故答案为：3
（
| 3a+1 |
| 3b+1 |
| 3c+1 |
=（1?
| 3a+1 |
| 3b+1 |
| 3c+1 |
≤（12+12+12）[（
| 3a+1 |
| 3b+1 |
| 3c+1 |
当且仅当
| 3a+1 |
| 3b+1 |
| 3c+1 |
即a=b=c=
| 1 |
| 3 |
| 3a+1 |
| 3b+1 |
| 3c+1 |
因此
| 3a+1 |
| 3b+1 |
| 3c+1 |
| 2 |
故答案为：3
| 2 |
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
）的直角坐标是 ．
，则线段CD的长为 ．
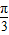）的直角坐标是 ．