题目内容
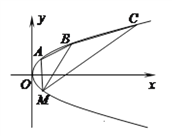
【题目】如图所示,倾斜角为![]() 的直线经过抛物线
的直线经过抛物线![]() 的焦点
的焦点![]() ,且与抛物线交于
,且与抛物线交于![]() 两点.
两点.

(1)求抛物线的焦点![]() 的坐标及准线
的坐标及准线![]() 的方程;
的方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 轴于点
轴于点![]() .证明
.证明![]() 为定值,并求此定值.
为定值,并求此定值.
【答案】(1)![]() ;
;![]() (2)证明见解析;定值为8
(2)证明见解析;定值为8
【解析】
(1)根据抛物线标准方程得![]() ,从而易得焦点坐标和准线方程;
,从而易得焦点坐标和准线方程;
(2)设点![]() 的坐标分别为
的坐标分别为![]() .直线
.直线![]() 的斜率为
的斜率为![]() ,则直线方程为
,则直线方程为![]() ,代入抛物线方程整理后可和
,代入抛物线方程整理后可和![]() ,这样可得
,这样可得![]() 中点
中点![]() 的坐标
的坐标![]() ,由直线
,由直线![]() 与
与![]() 垂直可得
垂直可得![]() 的方程,在此方程中令
的方程,在此方程中令![]() 得
得![]() ,计算化简
,计算化简![]() 得定值.
得定值.
解(1)设抛物线的标准方程为![]() ,则
,则![]() ,从而
,从而![]() .
.
因此焦点![]() 的坐标为(2,0),又准线方程的一般式为
的坐标为(2,0),又准线方程的一般式为![]() .
.
从而所求准线的方程为![]() .
.
(2)设点![]() 的坐标分别为
的坐标分别为![]() .直线
.直线![]() 的斜率为
的斜率为![]() ,则直线方程为
,则直线方程为![]() .将此式代入
.将此式代入![]() ,得
,得![]() .
.
故![]() .
.
记直线![]() 与
与![]() 的交点为
的交点为![]() ,则
,则![]() ,
,![]() .
.
故直线![]() 的方程为
的方程为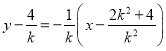 .
.
令![]() ,得点
,得点![]() 的横坐标
的横坐标![]() ,故
,故
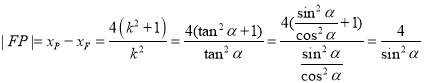 .
.
从而![]() 为定值.
为定值.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
【题目】为研究患肺癌与是否吸烟有关,某机构做了一次相关调查,制成如下图的![]() 列联表,其中数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的
列联表,其中数据丢失,但可以确定的是不吸烟人数与吸烟人数相同,吸烟患肺癌人数占吸烟总人数的![]() ;不吸烟的人数中,患肺癌与不患肺癌的比为
;不吸烟的人数中,患肺癌与不患肺癌的比为![]() .
.
患肺癌 | 不患肺癌 | 合计 | |
吸烟 | |||
不吸烟 | |||
总计 |
(1)若吸烟不患肺癌的有4人,现从患肺癌的人中用分层抽样的方法抽取5人,再从这5人中随机抽取2人进行调查,求这两人都是吸烟患肺癌的概率;
(2)若研究得到在犯错误概率不超过0.001的前提下,认为患肺癌与吸烟有关,则吸烟的人数至少有多少?
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |