题目内容

18．用诱导公式求下列三角值：
（1）cos（-$\frac{17π}{4}$）；                          
（2）sin（-1574°）；
（3）sin（-2160°52′）；
（4）cos（-1751°36′）
（5）cos1615°8′；
（6）sin（-$\frac{26}{3}π$）．

分析 直接利用诱导公式化简取值即可．

解答 解：（1）cos（-$\frac{17π}{4}$）=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$；             
（2）sin（-1574°）=-sin134°=-sin46°；
（3）sin（-2160°52′）=-sin0°52′；      
（4）cos（-1751°36′）=cos48°8′；
（5）cos1 615°8′=-cos4°52′；            
（6）sin（-$\frac{26}{3}$π）=-sin$\frac{2π}{3}$=-$\frac{\sqrt{3}}{2}$．

点评 本题考查三角函数的化简求值，基本知识的考查．

练习册系列答案
相关题目
1．已知sinα=3-a，求a的取值范围．
2．已知cos（$\frac{π}{4}$+α）=$\frac{5}{13}$，cos（$\frac{π}{4}$-β）=$\frac{3}{5}$，α∈（-$\frac{π}{4}$，$\frac{π}{4}$），β∈（$\frac{π}{4}$，$\frac{3π}{4}$）．
（1）求sinα的值；
（2）求cos（α-β）的值．
6．正方体的棱长为1，C、D、M分别为三条棱的中点，A、B是顶点，那么点M到截面ABCD的距离是（　　）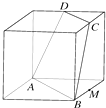 
A．$\frac{2}{3}$B．$\frac{1}{3}$C．$\frac{\sqrt{6}}{3}$D．$\frac{\sqrt{6}}{2}$
13．幂函数f（x）=xα（α为常数）的图象经过点（$\frac{1}{2}，\frac{1}{4}$）
（1）求函数f（x）的解析式；
（2）x∈[-1，1]时，函数y=f（x）-2ax+3的最小值为g（a），求g（a）的表达式；
（3）是否存在实数m＞n＞0，使得a∈[n，m]时，总有g（a）∈[n2，m2]成立，若存在，求出m，n的值，否则说明理由．
3．数字“2015”中，各位数字相加和为8，称该数为“如意四位数”，则用数字0，1，2，3，4，5组成的无重复数字且大于2015的“如意四位数”有（　　）个．
A．21B．22C．23D．24
10．已知函数y=f（x）的图象关于点（a，b）对称的充要条件是f（a+x）+f（a-x）=2b（或f（x）+f（2a-x）=2b）．如果函数y=f（x）的图象关于点（a，b）对称，则称点（a，b）为“中心点”，称函数y=f（x）为“准奇函数”．现有如下命题：
①若函数f（x）在R上的“中心点”为（a，f（a））则函数F（x）=f（x+a）-f（a）为R上的奇函数．
②若定义在R上的偶函数y=f（x）的“中心点”为（1，2），则方程f（x）=2在[-10，10]上至少有10个根．
③已知函数f（x）是定义在R上的增函数，点（1，0）为函数y=f（x-1）的“中心点”，若不等式f（m2-6m+21）+f（n2-8n）＜0对任意的m，n∈R恒成立，则当m＞3时，13＜m2+n2＜49．
其中正确的命题是①②③．（写出所有正确命题的序号）
7．函数f（x）=$\frac{a+lnx}{x}$，若曲线f（x）在点（e，f（e））处的切线与直线e2x-y+e=0垂直（其中e为自然对数的底数）．
（1）若f（x）在（m，m+1）上存在极值，求实数m的取值范围；
（2）求证：当x＞1时，$\frac{f（x）}{e+1}$＞$\frac{2{e}^{x-1}}{（x+1）（x{e}^{x}+1）}$．
8．已知函数f（x）=$\left\{\begin{array}{l}{x+2，x＞a}\\{{x}^{2}+5x+2，x≤a}\end{array}\right.$，函数g（x）=f（x）-2x恰有三个不同的零点，则实数a的取值范围是（　　）
A．[-1，1）B．[0，2]C．[-2，2）D．[-1，2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网