题目内容

18、如图，四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1，∠BAD=∠BAA1=∠DAA1=60°，O1为A1C1中点．
求证：AO1∥平面C1BD．
分析：欲证AO1∥平面C1BD，根据直线与平面平行的判定定理可知只需证AO1与平面C1BD内一直线平行即可，连接AC、BD交于O点，连接C1O，根据平行四边形的性质可知C1O∥AO1，C1O?平面C1BD，AO1?平面C1BD，满足定理条件．
解答：证明：连接AC、BD交于O点，连接C1O．
∵C1C∥A1A，∴四边形ACC1A1为平行四边形．
又O1，O分别为A1C1，AC的中点，
∴C1O∥AO1．
∵C1O?平面C1BD，AO1?平面C1BD，
∴AO1∥平面C1BD．
点评：本题主要考查了直线与平面平行的判定，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
相关题目
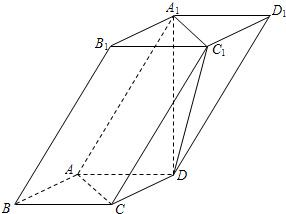精英家教网如图，四棱柱ABCD-A1B1C1D1中，A1D⊥平面ABCD，底面ABCD是边长为1的正方形，侧棱AA1=2．
（Ⅰ）求证：C1D∥平面ABB1A1；
（Ⅱ）求直线BD1与平面A1C1D所成角的正弦值；
（Ⅲ）求二面角D-A1C1-A的余弦值．
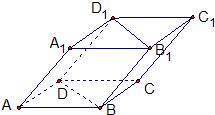精英家教网如图，四棱柱ABCD-A1B1C1D1的底面ABCD为正方形，侧棱与底面边长均为2a，且∠A1AD=∠A1AB=60°，则侧棱AA1和截面B1D1DB的距离是
 
．
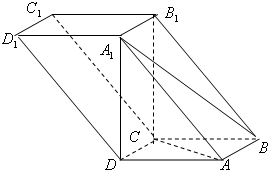精英家教网如图，四棱柱ABCD-A1B1C1D1中，A1D⊥平面ABCD，底面ABCD是边长为1的正方形，侧棱A1A=2，
（Ⅰ）证明：AC⊥A1B；
（Ⅱ）若棱AA1上存在一点P，使得
AP
=λ
PA1
，当二面角A-B1C1-P的大小为300时，求实数λ的值．
（2013•泉州模拟）如图，四棱柱ABCD-A1B1C1D1中，AA1⊥平面ABCD．
（Ⅰ）从下列①②③三个条件中选择一个做为AC⊥BD1的充分条件，并给予证明；
①AB⊥BC，②AC⊥BD；③ABCD是平行四边形．
（Ⅱ）设四棱柱ABCD-A1B1C1D1的所有棱长都为1，且∠BAD为锐角，求平面BDD1与平面BC1D1所成锐二面角θ的取值范围．
（2013•天津）如图，四棱柱ABCD-A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD=CD=1，
AA1=AB=2，E为棱AA1的中点．
（Ⅰ）证明B1C1⊥CE；
（Ⅱ）求二面角B1-CE-C1的正弦值．
（Ⅲ）设点M在线段C1E上，且直线AM与平面ADD1A1所成角的正弦值为
2
6
，求线段AM的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网