题目内容
若函数y=f(x)+sinx在区间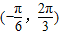 内单调递增,则f(x)可以是( )
内单调递增,则f(x)可以是( )A.sin(π-x)
B.cos(π-x)
C.
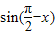
D.
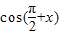
【答案】分析:利用四个选项代入f(x),分别求出函数y的解析式化简后,通过函数的单调增区间判断正确选项即可.
解答:解:对于A,y=f(x)+sinx=2sinx,显然函数在区间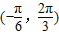 内x=
内x=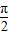 时函数取得最大值,函数存在增函数区间也存在减函数的区间,所以函数不单调递增,不正确;
时函数取得最大值,函数存在增函数区间也存在减函数的区间,所以函数不单调递增,不正确;
对于B,y=f(x)+sinx=sinx-cosx=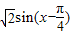 ,
,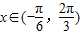 ,
,
所以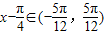 ,函数是单调增函数,正确.
,函数是单调增函数,正确.
对于C,y=f(x)+sinx=sinx+cosx=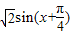 ,
,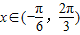 ,
,
所以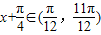 ,函数不是单调增函数,不正确.
,函数不是单调增函数,不正确.
对于D,y=f(x)+sinx=0,在区间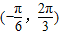 内单调递增,不正确;
内单调递增,不正确;
故选B.
点评:本题考查函数的解析式的求法,两角和与差的三角函数,三角函数的单调性的判断,考查计算能力.
解答:解:对于A,y=f(x)+sinx=2sinx,显然函数在区间
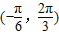 内x=
内x=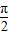 时函数取得最大值,函数存在增函数区间也存在减函数的区间,所以函数不单调递增,不正确;
时函数取得最大值,函数存在增函数区间也存在减函数的区间,所以函数不单调递增,不正确;对于B,y=f(x)+sinx=sinx-cosx=
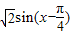 ,
,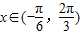 ,
,所以
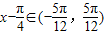 ,函数是单调增函数,正确.
,函数是单调增函数,正确.对于C,y=f(x)+sinx=sinx+cosx=
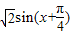 ,
,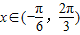 ,
,所以
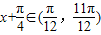 ,函数不是单调增函数,不正确.
,函数不是单调增函数,不正确.对于D,y=f(x)+sinx=0,在区间
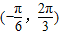 内单调递增,不正确;
内单调递增,不正确;故选B.
点评:本题考查函数的解析式的求法,两角和与差的三角函数,三角函数的单调性的判断,考查计算能力.

练习册系列答案
相关题目