题目内容
平面直角坐标系有点P(1,cosx),Q(cosx,1),x∈[-
,
];
(1)求向量
和
的夹角θ的余弦用x表示的函数f(x);
(2)求cosθ的最值.
| π |
| 4 |
| π |
| 4 |
(1)求向量
| OP |
| OQ |
(2)求cosθ的最值.
(1)∵P(1,cosx),Q(cosx,1),
∴
=(1,cosx),
=(cosx,1)
∴
•
=2cosx,|
||
|=1+cos2x
∴cosθ=
=
=f(x)
(2)f(x)=cosθ=
=
=
且x∈[-
,
]
∴cosθ∈[
,1]
令g(x)=x+
设x1,x2∈[
,1],且x1<x2
∵g′(x)=1-
<0在[
,1]上恒成立(此处也可以利用单调性的定义判断)
∴g(x)=x+
在[
,1]上是减函数.
∴2≤cosx+
≤
∴
≤f(x)≤1 即
≤cosθ≤1
∴
| OP |
| OQ |
∴
| OP |
| OQ |
| OP |
| OQ |
∴cosθ=
| ||||
|
|
| 2cosx |
| 1+cos2x |
(2)f(x)=cosθ=
| ||||
|
|
| 2cosx |
| 1+cos2x |
| 2 | ||
cosx+
|
| π |
| 4 |
| π |
| 4 |
∴cosθ∈[
| ||
| 2 |
令g(x)=x+
| 1 |
| x |
设x1,x2∈[
| ||
| 2 |
∵g′(x)=1-
| 1 |
| x2 |
| ||
| 2 |
∴g(x)=x+
| 1 |
| x |
| ||
| 2 |
∴2≤cosx+
| 1 |
| cosx |
3
| ||
| 2 |
∴
2
| ||
| 3 |
2
| ||
| 3 |

练习册系列答案
相关题目
 ,
, 和
和 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);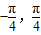 ];
];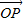 和
和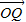 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x); ];
]; 和
和 的夹角θ的余弦用x表示的函数f(x);
的夹角θ的余弦用x表示的函数f(x);