题目内容
设f(x)=
,要使f (x)在(-∞,+∞)内连续,则a的值为( )
|
| A、0 | ||
| B、1 | ||
C、
| ||
| D、不存在 |
分析:本题解析式是一个分段函数,且其中一个在x=0处无定义,故需对此解析式进行恒等变形,利用极限的思想求出在x=0处的函数值,利用函数的连续性建立方程求解参数值.
解答:解:当x<0时,
=
=
故当x趋向于0时函数值趋向于
又f (x)在(-∞,+∞)内连续,故有
=a+0
解得a=
故选C
1-
| ||
| x |
| x | ||
x(1+
|
| 1 | ||
1+
|
| 1 |
| 2 |
又f (x)在(-∞,+∞)内连续,故有
| 1 |
| 2 |
解得a=
| 1 |
| 2 |
故选C
点评:本题考点是函数的连续性,考查通过函数的连续性得到相等关系,建立起关于参数的方程求参数,由于本题中的一段函数在端点处无意义,所以要对函数的解析式进行恒等变形,利用极限的思想求得端点函数值,建立方程求参数,在利用函数的连续性建立方程求参数时要注意此技巧的应用.

练习册系列答案
相关题目
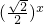 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是 ,1)
,1)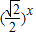 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)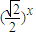 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)