题目内容
已知{an}为等差数列,Sn为其前n项和.若a1+a9=18,a4=7,则S10=
- A.55
- B.81
- C.90
- D.100
D
分析:利用等差数列的通项公式可得a1及公差d,再利用前n项和公式即可得到S10.
解答:设等差数列知{an}的公差为d,
∵a1+a9=18,a4=7,
∴ ,解得
,解得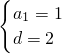 .
.
∴S10= =10×1+45×2=100.
=10×1+45×2=100.
故选D.
点评:熟练掌握等差数列的通项公式、前n项和公式是解题的关键.
分析:利用等差数列的通项公式可得a1及公差d,再利用前n项和公式即可得到S10.
解答:设等差数列知{an}的公差为d,
∵a1+a9=18,a4=7,
∴
 ,解得
,解得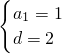 .
.∴S10=
 =10×1+45×2=100.
=10×1+45×2=100.故选D.
点评:熟练掌握等差数列的通项公式、前n项和公式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目