题目内容
(本小题满分12分)已知 且
且 ,函数
,函数 ,
,
(1)若 ,求函数
,求函数 的值域;
的值域;
(2)利用对数函数单调性讨论不等式 中
中 的取值范围.
的取值范围.
(1)当 时,函数
时,函数 的值域为
的值域为 ;
;
当 时,函数
时,函数 的值域为
的值域为
(2)见解析
【解析】
试题分析:(1)先求出 的定义域为
的定义域为 ,进而求出
,进而求出 的值域为
的值域为 ,
,
再分情况讨论 的值域;(2)根据底数a的范围来讨论函数函数的单调性,当
的值域;(2)根据底数a的范围来讨论函数函数的单调性,当 时,得
时,得 解得
解得 ,当
,当 ,得
,得 解得
解得 .
.
试题解析:(1)
由 得
得 ,所以函数
,所以函数 的定义域为
的定义域为
令 而
而 所以
所以
当 时,
时, 即
即
当 时,
时, 即
即
所以当 时,函数
时,函数 的值域为
的值域为 ;
;
当 时,函数
时,函数 的值域为
的值域为
(2)由 得
得 即
即 ①
①
当 时要使不等式①成立则
时要使不等式①成立则 即
即
当 时要使不等式①成立则
时要使不等式①成立则 即
即
综上所述
当 时不等式
时不等式 中
中 的取值范围为
的取值范围为 ;
;
当 时不等式
时不等式 中
中 的取值范围为
的取值范围为 .
.
考点:函数的定义,单调性,解不等式.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
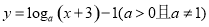 的图象恒过定点A,若点A也在函数
的图象恒过定点A,若点A也在函数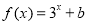 的图象上,则
的图象上,则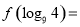 ( )
( ) 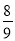 B.
B.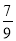 C.
C.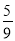 D.
D.
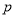 :实数m满足
:实数m满足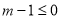 ,命题
,命题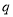 :函数
:函数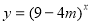 是增函数。若
是增函数。若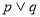 为真命题,
为真命题,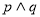 为假命题,则实数m的取值范围为( )
为假命题,则实数m的取值范围为( )
 B.
B. C.
C. D.
D.
 的图像关于原点对称,则
的图像关于原点对称,则 .
. 则
则 的值为( )
的值为( ) B.4 C.2 D.
B.4 C.2 D.
 及直线
及直线 截圆C所得的弦长均为10,则圆C的面积是 .
截圆C所得的弦长均为10,则圆C的面积是 . 、
、 ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
. 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;