题目内容
已知抛物线![]() :
:![]() 的焦点与椭圆
的焦点与椭圆![]() :
:![]() 的右焦点
的右焦点![]() 重合,
重合,![]() 是椭圆的左焦点.
是椭圆的左焦点.
(Ⅰ) 在![]() 中,若
中,若![]() ,
,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上运动,求
上运动,求![]() 重心
重心![]() 的轨迹方程;
的轨迹方程;
(Ⅱ) 若![]() 是抛物线
是抛物线![]() 与椭圆
与椭圆![]() 的一个公共点,且
的一个公共点,且![]() ,求
,求![]() 的值及
的值及![]() 的面积.
的面积.
解:(Ⅰ)设重心![]() ,
,![]() .
.
则 整理得
整理得  (
(![]() )
)
将(![]() )代入
)代入![]() 中,得
中,得![]()
所以,![]() 重心
重心![]() 的轨迹方程为
的轨迹方程为![]()
(Ⅱ) ∵椭圆与抛物线有共同的焦点,由![]() 得
得![]() ,
,
∴![]() 椭圆方程为
椭圆方程为![]() .
.
设![]() ,由
,由 得
得 ![]()
∴![]() (舍).
(舍).
∵![]() 是
是![]() 的准线,即抛物线的准线过椭圆的另一个焦点
的准线,即抛物线的准线过椭圆的另一个焦点![]() ,
,
设点![]() 到抛物线
到抛物线![]() 准线的距离为
准线的距离为![]() ,则
,则![]() .
.
又![]() ,
,
∴![]() ,
, ![]() .
.
过点![]() 作
作![]()
![]() 轴,垂足为
轴,垂足为![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ∴
∴![]() .
.
∴![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
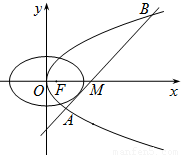
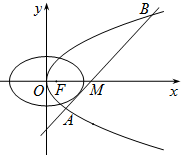 已知抛物线C1的焦点与椭圆C2:
已知抛物线C1的焦点与椭圆C2: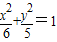 的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.
的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.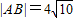 ,求直线l的方程.
,求直线l的方程.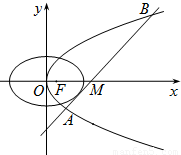
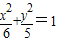 的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.
的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.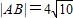 ,求直线l的方程.
,求直线l的方程.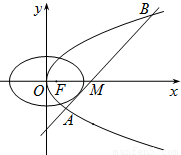
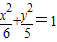 的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.
的右焦点重合,抛物线C1的顶点在坐标原点,过点M(4,0)的直线l与抛物线C1分别相交于A、B两点.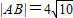 ,求直线l的方程.
,求直线l的方程.