Question

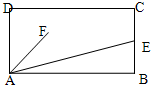如图，矩形ABCD中边长AB=2，BC=1，E为BC的中点，若F为正方形内（含边界）任意一点，则

AE

•

AF

的最大值为

9

2

．

Answer 1

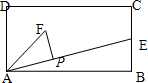
分析：画出向量在向量上的投影，推出F的位置，使得

AE

•

AF

的最大值，通过E，C的坐标，求出向量的数量积．

解答：解：因为

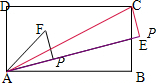
AE

•

AF

=|

AE

||

AF

|cos∠FAP=|

AE

||

AP

|，
如图，F在C位置时AP最大，
设AB为x轴，AD为y轴，则E（2，

1

2

），C（2，1）
所以

AE

•

AF

的最大值为：（2，

1

2

）•（2，1）=

9

2

．
故答案为：

9

2

．

点评：本题考查向量的数量积的应用，向量在向量方向上的投影的应用，考查计算能力．