题目内容
1.已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=|x-1|+|x-2|-3,若对任意实数x,恒有f(x-a)≤f(x),则非零实数a的取值范围为[6,+∞).分析 可以采用数形结合的方法解决,“对任意的x∈R,恒有f(x-a)≤f(x)”也就相当于在实数集R上,f(x-a)的图象恒在f(x)的图象下方,画出f(x)和f(x-a)的图象,据此列出关于a的不等式解出来即可.
解答 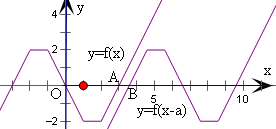 解:函数f(x)是定义在R上的奇函数,
解:函数f(x)是定义在R上的奇函数,
当x≥0时,f(x)=|x-1|+|x-2|-3,
当x<0时,-x>0,可得f(-x)=|-x-1|+|-x-2|-3=-f(x),
即有f(x)=3-|x+1|-|x+2|(x<0),
作出y=f(x)的图象,y=f(x-a)的图象可由f(x)的图象
平移可得.
由题意可得在实数集R上,f(x-a)的图象恒在f(x)的图象下,
所以只需y=f(x)与x轴最右边的交点A(3,0)
在y=f(x-a)与x轴最左边交点B(-3+a,0)的左边或重合.
因此应该有3≤-3+a,即a≥6.
故答案为:[6,+∞).
点评 这道题是将不等式恒成立问题转化为函数的最值问题,因为问题相对复杂,因此借助于数形结合,使得问题变得简单明了,注意此法适合于选择、填空题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
11.锐角△ABC中,角A,B,C的对边分别是a,b,c,若tanC=2,则$\frac{sinA}{sinB}$的取值范围是( )
| A. | ($\frac{{\sqrt{2}}}{2},\sqrt{2}$) | B. | ($\frac{{\sqrt{3}}}{3},\sqrt{3}$) | C. | (0,$\sqrt{5}$) | D. | ($\frac{1}{2},2$) |
6.已知sinα+sinβ+sinγ=0和cosα+cosβ+cosγ=0,则cos(α-β)的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |