题目内容
若f(x)=2sin(
x+φ),且f(1)=a,则f(5)=
| π | 2 |
a
a
.分析:根据题意将x=1代入表达式,结合诱导公式算出a=2cosφ,从而得到f(5)=2cosφ=a,得到本题的答案.
解答:解:∵f(1)=a,
∴2sin(
+φ)=a,可得a=2cosφ
因此,f(5)=2sin(
+φ)=2cosφ=a
故答案为:a
∴2sin(
| π |
| 2 |
因此,f(5)=2sin(
| 5π |
| 2 |
故答案为:a
点评:本题给出三角函数式,在已知f(1)=a的情况下求f(5)的值,着重考查了三角函数的诱导公式的知识,属于基础题.

练习册系列答案
相关题目
 上的最大值为
上的最大值为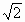 ,则w
=________.
,则w
=________. 上的最大值是
上的最大值是 ,则w
______.
,则w
______.