题目内容
如图,正四棱柱ABCD—A1B(1)求证:BD⊥平面AA
(2)求线段PQ中点M所形成图形的面积;
(3)若PA=![]() ,当四面体B—QDC1的体积最小时,求二面角B-C1Q-C的大小.
,当四面体B—QDC1的体积最小时,求二面角B-C1Q-C的大小.
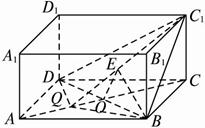
(1)证明:∵四边形ABCD为正方形,?
∴BD⊥AC,AA1⊥面BD,?
BD![]() 面ABCD,BD⊥AA1,?
面ABCD,BD⊥AA1,?
∴BD⊥平面ACC
 ?
?
(2)解:∵AA1⊥平面ABCD,∴AA1⊥AQ.?
M为PQ中点,AM=1, ?
点M在以A为球心,半径为1的球面上,动点M所形成图形的面积为S=![]() . ?
. ?
(3)解:若PA=![]() ,则AQ=
,则AQ=![]() .Q在以A为圆心,半径为
.Q在以A为圆心,半径为![]() 的圆弧上运动.?
的圆弧上运动.?
∵V![]() =V
=V![]() ,C1到面BDQ的距离为2,只要S△BDQ面积最小即可,即Q到BD距离最小.
,C1到面BDQ的距离为2,只要S△BDQ面积最小即可,即Q到BD距离最小.
?
∵AC⊥BD,∴Q在AC上.?
设BD∩AC=O,BD⊥平面CC1Q,过O作OE⊥C1Q交C1Q于E.连结BE,则∠BEO为二面角B-C1Q-C的平面角. ?
CQ=3![]() ,QO=
,QO=![]() ,C1Q=
,C1Q=![]() ,RT△OEQ∽RT△C1CQ?,?
,RT△OEQ∽RT△C1CQ?,?
∴OE=![]() ,tan∠BEO=
,tan∠BEO=![]() =
=![]() ,?
,?
∠BEO=arctan![]() .?
.?
∴二面角B-C1Q-C大小为arctan![]() .
.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案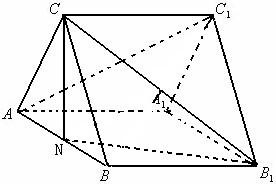 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
