题目内容
求
的值.
思路分析：观察被求式的函数名称的特点和角的特点，其中7°=15°-8°，15°=8°+?7°，8°=15°-7°.无论采取哪种代换方式，都可减少角的个数.利用和角或差角公式展开，进行约分，化简求值.若用7°=15°-8°代换，分子、分母是二次齐次式；若用15°=8°+7°或8°=15°-7°代换，分子、分母将会出现三次式，显然选择前者更好，不妨比较一下.
解法一：原式=
=
=
=tan15°=tan（45°-30°）
=
.
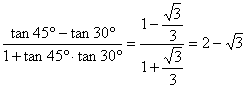解法二：原式=
=
=
=
=
=
=tan15°=
.
深化升华 三角函数式的结构一般由角、三角函数的符号及运算符号三部分组成，解题的突破口应从这三个方面入手，无论是化简、求值，还是证明，其结果应遵循以下几个原则：
（1）能求值的要求值；
（2）三角函数的种类尽可能少；
（3）角的种类尽可能少；
（4）次数尽可能低；
（5）尽可能不含根号和分母.
练习册系列答案
相关题目
如图，在平面直角坐标系中，以原点为圆心，单位长度1为半径的圆上有两点A（cosα，sinα），B（cosβ，sinβ）．（0＜α＜β＜π）