题目内容
3、函数f(x)=ax3+bx2-2x(a、b∈R且ab≠0)的图象如如图所示,且x1+x2<0,则有( )
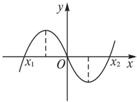

分析:由图象可以看出函数相应的方程有三个根,故可将其方程设为f(x)=ax(x-x1)(x-x2),由图象可以判断出,参数a>0,再由同一性可知b=-a(x1+x2),进而可以判断出参数b的取值范围.
解答:解:由题图可设设f(x)=ax(x-x1)(x-x2)
=ax[x2-(x1+x2)x+x1x2]
=ax3-a(x1+x2)x2+ax1x2x
=ax3+bx2-2x,
故b=-a(x1+x2),ax1x2=-2
由题中图象,知当x>x2>0时,f(x)>0,且x-x1>0,
∴a>0.
又∵x1+x2<0,
∴b=-a(x1+x2)>0.
故有a>0,b>0
故选A.
=ax[x2-(x1+x2)x+x1x2]
=ax3-a(x1+x2)x2+ax1x2x
=ax3+bx2-2x,
故b=-a(x1+x2),ax1x2=-2
由题中图象,知当x>x2>0时,f(x)>0,且x-x1>0,
∴a>0.
又∵x1+x2<0,
∴b=-a(x1+x2)>0.
故有a>0,b>0
故选A.
点评:本题考点是函数的图象,考查由函数的图象的特征判断出函数的参数的取值范围.本题综合性较强,要注意挖掘图象中的每一个特征,将其转化为方程或不等式,研究参数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目