题目内容
若任取x1、x2∈[a,b],且x1≠x2,都有f(
)>
成立,则称f(x) 是[a,b]上的凸函数.试问:在下列图象中,是凸函数图象的为( )
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
A. | B. α | C. | D. |
∵任取x1、x2∈[a,b],且x1≠x2,都有f(
)>
成立
∴函数f(x)是[a,b]上的凸函数
任取x1、x2∈[a,b],且x1≠x2,
则A中,f(
)=
成立,故A不满足要求;
则B中,f(
)<
成立,故B不满足要求;
则C中,f(
)>
成立,故C满足要求;
则D中,f(
)与
大小不确定,故D不满足要求;
故选C
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
∴函数f(x)是[a,b]上的凸函数
任取x1、x2∈[a,b],且x1≠x2,
则A中,f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
则B中,f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
则C中,f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
则D中,f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
故选C

练习册系列答案
相关题目
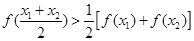 成立,则称f(x)
成立,则称f(x)
