题目内容
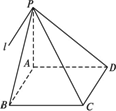
如下图,过正方形ABCD的顶点A作PA⊥平面ABCD,若PA=AB,则平面ABP与平面CDP所成的二面角的度数是
[ ]
A.30°
B.45°
C.60°
D.90°
答案:B
解析:
解析:
|
PAB面与CDP面所成的二面角为无棱二面角,首先作出二面角的棱,∵AB∥CD, ∴(如题图)过P点作直线l∥AB,则l为所求二面角的棱. ∵PA⊥平面ABCD,∴AB⊥PA,∵AB⊥AD,∴AB⊥平面PAD. ∵l∥AB,∴l⊥平面PAD, ∴∠APD即为所求二面角的平面角, 即∠APD=45° |

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目