题目内容
 如图,A、B分别是射线OM,ON上的两点,给出下列向量:
如图,A、B分别是射线OM,ON上的两点,给出下列向量:
① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ .
.
这些向量中以O为起点,终点在阴影区域内的是
- A.①②
- B.①④
- C.①③
- D.⑤
C
分析:题目中要我们判断向量的线性运算结果的情况,这样的题目需要对五个结论挨个验证,①过A作ON的平行线AC,并且使得AC=2OB,根据向量加法的三角形法则,得到和的重点在阴影里,①符合要求.用同样的方法验证其他几个的结果.
解答:∵过A作ON的平行线AC,并且使得AC=2OB,
根据向量加法的三角形法则,得到和的重点在阴影里.
故①符合要求,排除D答案,
∵取OA的中点D,过D作DE平行于ON,使得DE= OB,
OB,
∵过D且与ON平行的线交AB于F,DF= OB
OB
∴DE<DF,
∴F不在阴影里,排除A,
在OA上取点H,使得AH= OA,
OA,
过H作OB的平行线交AB于I,
则HI= OB<
OB< OB,
OB,
③符合要求,
故选C.
点评:向量是集数与形于一身的数学概念,是数学中数形结合思想的体现,向量也是重要的物理模型,在实际生活中有着广泛的应用,它是高中数学的基础.
分析:题目中要我们判断向量的线性运算结果的情况,这样的题目需要对五个结论挨个验证,①过A作ON的平行线AC,并且使得AC=2OB,根据向量加法的三角形法则,得到和的重点在阴影里,①符合要求.用同样的方法验证其他几个的结果.
解答:∵过A作ON的平行线AC,并且使得AC=2OB,
根据向量加法的三角形法则,得到和的重点在阴影里.
故①符合要求,排除D答案,
∵取OA的中点D,过D作DE平行于ON,使得DE=
 OB,
OB,∵过D且与ON平行的线交AB于F,DF=
 OB
OB∴DE<DF,
∴F不在阴影里,排除A,
在OA上取点H,使得AH=
 OA,
OA,过H作OB的平行线交AB于I,
则HI=
 OB<
OB< OB,
OB,③符合要求,
故选C.
点评:向量是集数与形于一身的数学概念,是数学中数形结合思想的体现,向量也是重要的物理模型,在实际生活中有着广泛的应用,它是高中数学的基础.

练习册系列答案
相关题目
 ,2)的入射光线 l1
,2)的入射光线 l1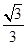 x反射.反射光线l2交y轴于B点,圆C过点A且与l1, l2都相切.
x反射.反射光线l2交y轴于B点,圆C过点A且与l1, l2都相切.
 分别是直线l和圆C上的动点,求
分别是直线l和圆C上的动点,求 的最小值及此时点
的最小值及此时点 的坐标.
的坐标.