题目内容
在平面直角坐标系xOy中,函数f(x)=asinax+cosax(a>0)在一个最小正周期长的区间上的图象与函数g(x)= 的图象所围成的封闭图形的面积是________.
的图象所围成的封闭图形的面积是________.

 .
.分析:首先由三角函数的知识把函数化简为y=Asin(wx+Φ)的形式.解法一:由图象的对称性,把要求的面积转化为长为
 ,宽为2
,宽为2 的矩形面积的一半来解决;解法二,用定积分的意义转化为定积分
的矩形面积的一半来解决;解法二,用定积分的意义转化为定积分
 [1-sin(ax+?)]dx来求解.
[1-sin(ax+?)]dx来求解.解答:
 解法一:由三角函数公式可得f(x)=asinax+cosax=
解法一:由三角函数公式可得f(x)=asinax+cosax= sin(ax+?),其中tan?=
sin(ax+?),其中tan?= ,
,所以函数的周期为T=
 ,取长为
,取长为 ,宽为2
,宽为2 的矩形,
的矩形,由对称性知,面积的一半即为所求.
故答案为:

 .
.解法二:由定积分的意义知,封闭图形的面积为

 [1-sin(ax+?)]dx
[1-sin(ax+?)]dx换元,令ax+?=t,则x=
 (t-?),上式可化为:
(t-?),上式可化为:
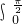 (1-sint)dt=
(1-sint)dt=

故答案为:

 .
.点评:本题考查曲边图形的面积,用定积分的定义或图象的对称性可解,属基础题.

练习册系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.