题目内容
【题目】已知长度为![]() 的线段
的线段![]() 的两个端点
的两个端点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上运动,动点
轴上运动,动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() ,且斜率不为零的直线
,且斜率不为零的直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,在
,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数?若存在,求出定点
的斜率之积为常数?若存在,求出定点![]() 的坐标以及此常数;若不存在,请说明理由.
的坐标以及此常数;若不存在,请说明理由.
【答案】(1)![]() (2)存在两个定点
(2)存在两个定点![]() ,
,![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,当定点为
的斜率之积为常数,当定点为![]() 时,常数为
时,常数为![]() ,当定点为
,当定点为![]() 时,常数为
时,常数为![]()
【解析】
(1)设![]() ,
,![]() ,
,![]() ,利用向量关系
,利用向量关系![]() 坐标化,可得曲线
坐标化,可得曲线![]() 的方程;
的方程;
(2)由题意设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,假设存在定点
,假设存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,将
的斜率之积为常数,将![]() 表示成关于
表示成关于![]() 的函数,利用恒成立问题,可得定点坐标.
的函数,利用恒成立问题,可得定点坐标.
(1)设![]() ,
,![]() ,
,![]() ,
,
由于![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以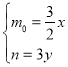 .又因为
.又因为![]() ,所以
,所以![]() ,
,
从而![]() ,即曲线
,即曲线![]() 的方程为
的方程为![]() .
.
(2)由题意设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
由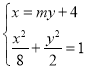 得
得![]() ,所以
,所以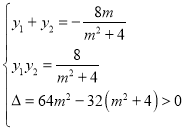 ,
,
故![]() ,
,![]() .
.
假设存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,则
的斜率之积为常数,则
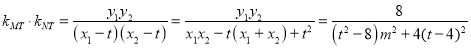 .
.
当![]() ,且
,且![]() 时,
时,![]() 为常数,解得
为常数,解得![]() .
.
显然当![]() 时,常数为
时,常数为![]() ;当
;当![]() 时,常数为
时,常数为![]() .
.
所以存在两个定点![]() ,
,![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数,当定点为
的斜率之积为常数,当定点为![]() 时,常数为
时,常数为![]() ,当定点为
,当定点为![]() 时,常数为
时,常数为![]() .
.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
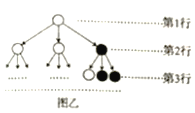
新黄冈兵法密卷系列答案【题目】杨辉三角,是二项式系数在三角形中的一种几何排列.中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现了杨辉三角.在欧洲,帕斯卡在1654年也发现了这一规律,所以这个表又叫做帕斯卡三角形.杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合.
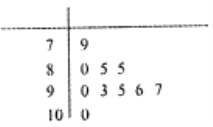
第0行 | 1 |
第1行 | 1 1 |
第2行 | 1 2 1 |
第3行 | 1 3 3 1 |
第4行 | 1 4 6 4 1 |
第5行 | 1 5 10 10 5 1 |
第6行 | 1 6 15 20 15 6 1 |
(1)记杨辉三角的前n行所有数之和为![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)在杨辉三角中是否存在某一行,且该行中三个相邻的数之比为![]() ?若存在,试求出是第几行;若不存在,请说明理由;
?若存在,试求出是第几行;若不存在,请说明理由;
(3)已知n,r为正整数,且![]() .求证:任何四个相邻的组合数
.求证:任何四个相邻的组合数![]() ,
,![]() ,
,![]() ,
,![]() 不能构成等差数列.
不能构成等差数列.