题目内容
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,∠BAD=60°.
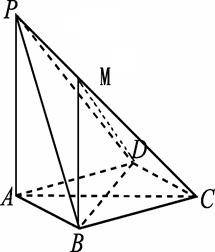
(Ⅰ)求证:直线BD⊥平面PAC;
(Ⅱ)求直线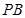 与平面
与平面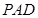 所成角的正切值;
所成角的正切值;
(Ⅲ)已知M在线段PC上,且BM=DM= ,CM=3,求二面角
,CM=3,求二面角 的余弦值.
的余弦值.

(Ⅰ)求证:直线BD⊥平面PAC;
(Ⅱ)求直线
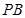 与平面
与平面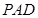 所成角的正切值;
所成角的正切值;(Ⅲ)已知M在线段PC上,且BM=DM=
 ,CM=3,求二面角
,CM=3,求二面角 的余弦值.
的余弦值.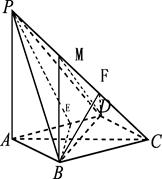
(Ⅰ)证明:因为四边形ABCD是菱形, 所以AC⊥BD. ………………1分
又因为PA⊥平面ABCD,
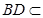 平面ABCD, 所以PA⊥BD, …3分
平面ABCD, 所以PA⊥BD, …3分又因为
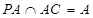 ,所以BD⊥平面PAC. ………………4分
,所以BD⊥平面PAC. ………………4分(Ⅱ)
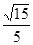
(Ⅲ)
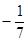
(I)由条件易知AC⊥BD,然后再证PA⊥BD即可.
(II)本小题关键是找或做出PB与平面PAD所成的角,过B作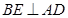 ,连结PE,
,连结PE,
因为PA⊥平面ABCD,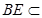 平面ABCD, 所以PA⊥BE,又因为
平面ABCD, 所以PA⊥BE,又因为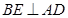 ,
,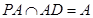 ,所以BE⊥平面PAD.所以
,所以BE⊥平面PAD.所以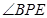 是直线
是直线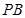 与平面
与平面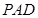 所成角.过B作
所成角.过B作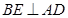 ,连结PE,
,连结PE,
因为PA⊥平面ABCD,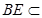 平面ABCD, 所以PA⊥BE
平面ABCD, 所以PA⊥BE
又因为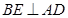 ,
,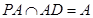 ,所以BE⊥平面PAD. ………………5分
,所以BE⊥平面PAD. ………………5分
所以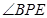 是直线
是直线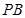 与平面
与平面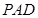 所成角. ………………6分
所成角. ………………6分
在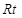 △BEP中,
△BEP中,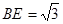 ,
,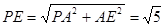 , ………………7分
, ………………7分
所以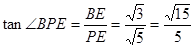 .
.
所以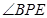 是直线
是直线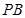 与平面
与平面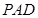 所成角的正切值
所成角的正切值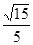 . ………………8分
. ………………8分
(Ⅲ)设F是MC的中点,连结BF,DF,
因为BM=BC,△BMC为等腰△,
所以BF⊥MC 同理DF⊥MC ………………9分
所以 为二面角
为二面角 的平面角.………10分
的平面角.………10分
在△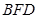 中,
中,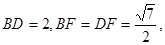 ………………11分
………………11分
由余弦定理得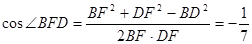 .
.
所以二面角 的余弦值为
的余弦值为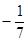 .………………12分
.………………12分
(II)本小题关键是找或做出PB与平面PAD所成的角,过B作
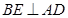 ,连结PE,
,连结PE,因为PA⊥平面ABCD,
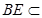 平面ABCD, 所以PA⊥BE,又因为
平面ABCD, 所以PA⊥BE,又因为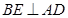 ,
,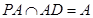 ,所以BE⊥平面PAD.所以
,所以BE⊥平面PAD.所以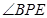 是直线
是直线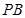 与平面
与平面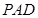 所成角.过B作
所成角.过B作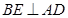 ,连结PE,
,连结PE,因为PA⊥平面ABCD,
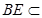 平面ABCD, 所以PA⊥BE
平面ABCD, 所以PA⊥BE又因为
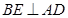 ,
,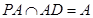 ,所以BE⊥平面PAD. ………………5分
,所以BE⊥平面PAD. ………………5分所以
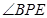 是直线
是直线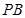 与平面
与平面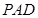 所成角. ………………6分
所成角. ………………6分在
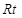 △BEP中,
△BEP中,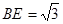 ,
,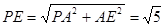 , ………………7分
, ………………7分所以
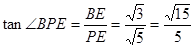 .
.所以
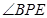 是直线
是直线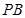 与平面
与平面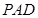 所成角的正切值
所成角的正切值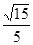 . ………………8分
. ………………8分(Ⅲ)设F是MC的中点,连结BF,DF,
因为BM=BC,△BMC为等腰△,
所以BF⊥MC 同理DF⊥MC ………………9分
所以
 为二面角
为二面角 的平面角.………10分
的平面角.………10分在△
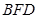 中,
中,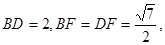 ………………11分
………………11分由余弦定理得
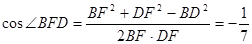 .
.所以二面角
 的余弦值为
的余弦值为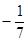 .………………12分
.………………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
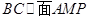 ;(Ⅱ)求证:平面MAP⊥平面SAC;
;(Ⅱ)求证:平面MAP⊥平面SAC;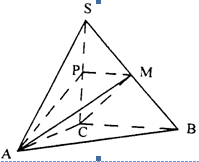
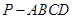 中,
中, 底面
底面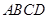 ,四边形
,四边形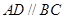 ,
,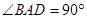 ,
, ,
,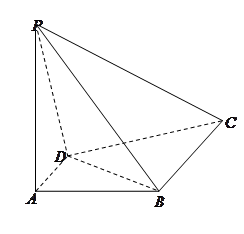
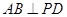 ;
;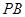 上找出一点
上找出一点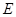 ,使
,使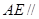 平面
平面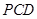 ,
,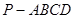 中,
中,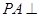 平面
平面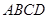 ,底面
,底面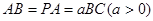 .
.
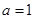 时,求证:
时,求证: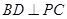 ;
;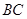 边上有且只有一个点
边上有且只有一个点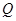 ,使得
,使得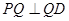 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.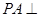 平面
平面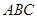 ,
,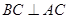 ,则图中直角三角形的个数为________.
,则图中直角三角形的个数为________.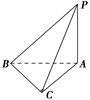
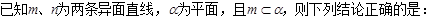 ( )
( )
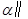 平面
平面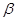 的是( )
的是( )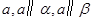
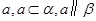
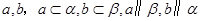
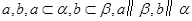
 、
、 是两个不同的平面,
是两个不同的平面,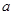 、
、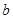 是两条不同的直线,给出下列4个命题,其中正确命题是( )
是两条不同的直线,给出下列4个命题,其中正确命题是( )