Question

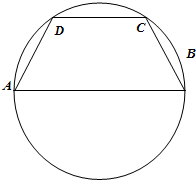已知线段AB的长为4，以AB为直径的圆有一内接梯形ABCD，其中AB∥CD（如图）则这个梯形的周长的最大值为（　　）

• A、8
• B、10
• C、4(

  2

  +1)
• D、以上都不对

Answer 1

分析：如图所示，设∠DOA=θ，(0＜θ＜

π

2

)．作DQ⊥AB，垂足为Q．则DQ=2sinθ，OQ=2cosθ．利用勾股定理及其三角函数的基本关系式、倍角公式可得AD=

QD2+AQ2

=4sin

θ

2

．利用DC∥AB，可得AD=BC．利用倍角公式于是梯形ABCD的周长l=AB+2AD+DC=-8(sin

θ

2

-

1

2

)2+10，再利用二次函数的单调性即可得出．

解答：解：如图所示，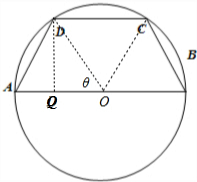
设∠DOA=θ，(0＜θ＜

π

2

)．作DQ⊥AB，垂足为Q．
则DQ=2sinθ，OQ=2cosθ．
∴AQ=2-OQ=2-2cosθ，
∴AD=

QD2+AQ2

=

(2sinθ)2+(2-2cosθ)2

=

4sin2θ+4cos2θ-8cosθ+4

=

8-8cosθ

=

8×2sin2 θ 2

=4sin

θ

2

．
∵DC∥AB，∴AD=BC．
∴梯形ABCD的周长l=AB+2AD+DC
=4+8sin

θ

2

+4cosθ
=8sin

θ

2

+4(1-2sin2

θ

2

)+4
=-8(sin

θ

2

-

1

2

)2+10
当且仅当sin

θ

2

=

1

2

，即θ=

π

3

时取等号．
∴梯形ABCD的周长的最大值为10．
故选：B．

点评：本题考查了圆的性质、勾股定理及其三角函数的基本关系式、倍角公式、二次函数的单调性等基础知识与基本技能方法，考查了分析问题和解决问题的能力，考查了计算能力，属于难题．