题目内容
 设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,f(2)=0.求不等式(x-1)•f(x-1)<0的解集.
设奇函数f(x)的定义域为[-5,5],若当x∈[0,5]时,f(x)的图象如图,f(2)=0.求不等式(x-1)•f(x-1)<0的解集.分析:先将x-1看作整体.根据函数f(x)在x∈[0,5]的图象再结合奇函数f(x)的性质,可分析出当x∈[-,5,0)的函数值f(x)的正负情况,然后利用分类讨论的方法即可求解不等式(x-1)•f(x-1)<0.
解答:解:根据当x∈[0,5]时f(x)的图象可知当0<x<2时f(x)>0,当2<x≤5时f(x)<0,
且f(x)为奇函数,∴当-2<x<0时f(x)<0,当-5≤x<-2时f(x)>0.
∵(x-1)•f(x-1)<0
∴
或
即
或
解得3<x≤6或-4<x≤-1,
∴原不等式的解集为(3,6]∪[-4,-1).
且f(x)为奇函数,∴当-2<x<0时f(x)<0,当-5≤x<-2时f(x)>0.
∵(x-1)•f(x-1)<0
∴
|
|
即
|
|
解得3<x≤6或-4<x≤-1,
∴原不等式的解集为(3,6]∪[-4,-1).
点评:本题主要考查了利用函数的图象和函数的性质(奇偶性)求解抽象不等式xf(x)<0.解题的关键是根据函数的奇偶性分析出x∈[-5,0)的函数值f(x)的正负情况.本题也可利用奇函数图象关于原点对称作出y轴左侧的图象,根据图象写出解集.

练习册系列答案
相关题目
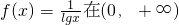 是减函数;
是减函数;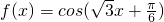 ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数;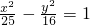 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5; 是减函数;
是减函数; ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数; 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5;