题目内容

（2010•浙江模拟）已知向量
a
=（1，1），
b
=（2，n），若|
a
+
b
|=
a
•
b
，则实数n的值是（　　）
分析：求出
a
+
b
的坐标，向量的模的定义求出|
a
+
b
|，再由两个向量的数量积公式求出
a
•
b
，由|
a
+
b
|=
a
•
b
得到
9+(n+1)2
=2+n，解方程求出实数n的值．
解答：解：由题意可得
a
+
b
=（3，n+1），∴|
a
+
b
|=
9+(n+1)2
，
a
•
b
=2+n．
由|
a
+
b
|=
a
•
b
，可得
9+(n+1)2
=2+n，化简可得 n2+2n+10=n2+4n+4，
解得 n=3，
故选C．
点评：本题主要考查两个向量的数量积公式，两个向量坐标形式的运算，向量的模的定义和求法，属于基础题．
练习册系列答案
相关题目
（2010•浙江模拟）设函数f(x)=2cos2x+2
3
sinxcosx+m(x∈R)
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）若x∈[0，
π
2
]，是否存在实数m，使函数f（x）的值域恰为[
1
2
，
7
2
]？若存在，请求出m的取值；若不存在，请说明理由．
（2010•浙江模拟）如果数列{an}满足：首项a1=1且an+1=
2an，n为奇数
an+2，n为偶数
那么下列说法中正确的是（　　）
（2010•浙江模拟）设i为虚数单位，则(
1+ii
)4=
-4
-4
．
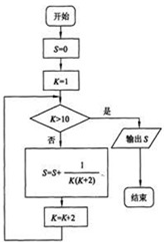（2010•浙江模拟）若某一程序框图如图所示，则该程序运行后输出的S等于
5
11
5
11
．
（2010•浙江模拟）已知四棱锥P-ABCD，底面是边长为1的正方形，侧棱PC长为2，且PC⊥底面ABCD，E是侧棱PC上的动点．
（Ⅰ）不论点E在何位置，是否都有BD⊥AE？证明你的结论；
（Ⅱ）求点C到平面PDB的距离；
（Ⅲ）若点E为PC的中点，求二面角D-AE-B的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网