题目内容
已知抛物线的顶点在坐标原点,焦点在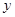 轴上,且过点
轴上,且过点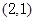 .
.
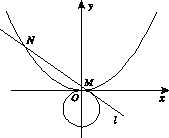
(Ⅰ)求抛物线的标准方程;
(Ⅱ)与圆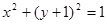 相切的直线
相切的直线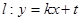 交抛物线于不同的两点
交抛物线于不同的两点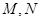 若抛物线上一点
若抛物线上一点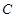 满足
满足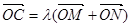
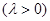 ,求
,求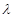 的取值范围.
的取值范围.
 轴上,且过点
轴上,且过点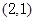 .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)与圆
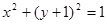 相切的直线
相切的直线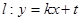 交抛物线于不同的两点
交抛物线于不同的两点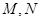 若抛物线上一点
若抛物线上一点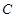 满足
满足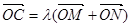
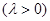 ,求
,求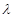 的取值范围.
的取值范围.(Ⅰ)  ; (Ⅱ)
; (Ⅱ)  .
.
 ; (Ⅱ)
; (Ⅱ)  .
.试题分析:(Ⅰ) 由题意设抛物线的标准方程,把已知点代入解得抛物线的标准方程;(Ⅱ)先由直线与圆相切得圆心到直线的距离为圆的半径,可得
 与
与 的关系式,在把直线方程与抛物线方程联立方程组整理为关于
的关系式,在把直线方程与抛物线方程联立方程组整理为关于 的方程,利用判别式大于0求得
的方程,利用判别式大于0求得 的取值范围,并设出交点
的取值范围,并设出交点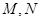 的坐标,由根与系数的关系式和已知向量的关系式,把
的坐标,由根与系数的关系式和已知向量的关系式,把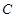 点的坐标表示出来,再代入抛物线方程,把
点的坐标表示出来,再代入抛物线方程,把 用
用 表示出来,从而可得
表示出来,从而可得 的取值范围.
的取值范围.试题解析:(Ⅰ) 设抛物线方程为
 , 由已知得:
, 由已知得: , 所以
, 所以 ,
,所以抛物线的标准方程为
 . 4分
. 4分(Ⅱ) 因为直线与圆相切, 所以
 , 6分
, 6分把直线方程代入抛物线方程并整理得:
 , 7分
, 7分由
 , 得
, 得  或
或 , 8分
, 8分设
 , 则
, 则 ,
, ,
,由
 ,
,得
 , 11分
, 11分因为点
 在抛物线
在抛物线 上,所以,
上,所以,
 , 13分
, 13分因为
 或
或 ,所以
,所以  或
或  ,
,所以
 的取值范围为
的取值范围为  . 15分
. 15分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
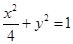 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.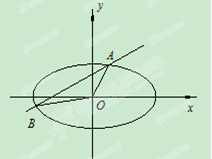
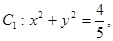 直线
直线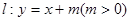 与圆
与圆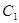 相切,且交椭圆
相切,且交椭圆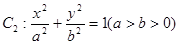 于
于 两点,
两点,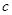 是椭圆的半焦距,
是椭圆的半焦距,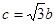 ,
,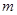 的值;
的值;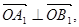 求椭圆
求椭圆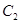 的方程;
的方程;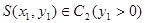 ,直线AS,BS与直线
,直线AS,BS与直线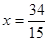 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.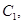 抛物线
抛物线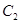 的焦点均在
的焦点均在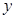 轴上,
轴上,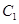 的中心和
的中心和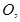 从每条曲线上取两个点,将其坐标记录于下表中:
从每条曲线上取两个点,将其坐标记录于下表中: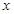
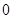
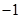
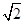
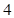
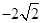
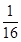
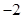
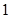
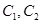 的方程的点的坐标;
的方程的点的坐标;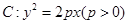 的焦点为
的焦点为 ,准线为
,准线为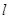 ,
,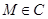 ,以
,以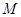 为圆心的圆
为圆心的圆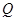 ,
,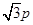 ,
,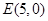 是圆
是圆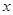 轴除
轴除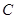 与圆
与圆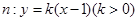 ,
,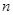 与
与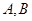 两点,
两点,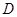 ,且
,且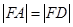 , 求
, 求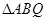 的面积.
的面积. 以椭圆
以椭圆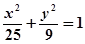 的两个焦点为焦点,且双曲线
的两个焦点为焦点,且双曲线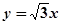 ,
,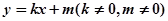 与双曲线
与双曲线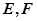 ,且
,且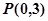 为圆心的圆上,求实数
为圆心的圆上,求实数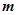 的取值范围.
的取值范围.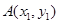 ,
,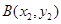 是抛物线
是抛物线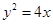 上相异两点,且满足
上相异两点,且满足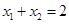 .
.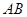 的中垂线经过点
的中垂线经过点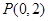 ,求直线
,求直线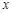 轴于点
轴于点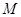 ,求
,求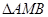 的面积的最大值及此时直线
的面积的最大值及此时直线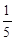
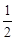
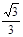
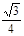
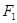 、
、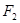 为双曲线
为双曲线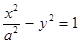 的两个焦点,点
的两个焦点,点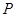 在此双曲线上,
在此双曲线上,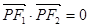 ,如果此双曲线的离心率等于
,如果此双曲线的离心率等于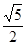 ,那么点
,那么点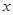 轴的距离等于 .
轴的距离等于 .