题目内容
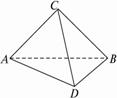
如右图,平面ABC⊥平面ABD,∠ACB=90°,CA=CB,△ABD是正三角形,则二面角G-BD-A的平面角的正切值为_________.
解析:
过C点作CO⊥AB,垂足为O,作OH⊥BD,垂足为H,连结CH.
∵平面ABC⊥平面ABD,交线为AB,
∴CO⊥平面ABD.
∴CO⊥BD.
又∵OH⊥BD,OH∩OC=O,
∴BD⊥平面COH.
∴BD⊥CH.
∴∠CHO为二面角C-BD-A的平面角.
设AC=CB=a,
则AB=BD=AD=2a,
.
∴
.
∴
.∴应填.
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如左图所示，直角梯形ABCD中，AD∥BC，∠ABC=90°，E、F分别是边AD和BC上的点，且EF∥AB，AD=2AE=2AB=4FC=4，将四边形EFCD沿EF折起使AE=AD，如右图所示．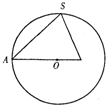
已知正三棱锥S-ABC内接于半径为6的球，过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图，则此三棱锥的侧面积为
，D、E分别是AC1和BB1的中点，则直线DE与平面BB1C1C所成的角为 ( )
B. 
C. 
D. 
，A、B、C、D为空间四点．在△ABC中，AB＝2，AC＝BC＝.等边三角形ADB以AB为轴运动．