题目内容
图形F1上的任一点与图形F2上的任一点的距离中的最小值,叫做图形F1与图形F2的距离.(1)求图形y≥2x与图形y≤cosx的距离;
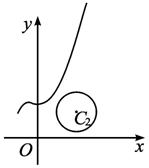
(2)已知曲线C1:y=![]() +1与圆C2:(x-1)2+(y-1)2=r2(r>0)的距离为
+1与圆C2:(x-1)2+(y-1)2=r2(r>0)的距离为![]() ,求r的值.
,求r的值.
解:(1)点P(0,1)同时落在这两个图形上,
∴这两个图形之间的距离为0.
(2)M(x,y)是曲线C1上任意一点,
则y=![]() +1(x≥-
+1(x≥-![]() ).
).
C2(1,1)是⊙C2的圆心,
记f(x)=|C2M|2,
则f(x)=(x-1)2+(y-1)2=x2-2x+1+4(x3+![]() )=4x3+x2-2x+
)=4x3+x2-2x+![]() (x≥-
(x≥-![]() ).
).
f′(x)=12x2+2x-2=12(x-![]() )(x+
)(x+![]() ).
).
令f′(x)=0,得x=![]() .
.
当-![]() ≤x<
≤x<![]() 时,f′(x)<0,
时,f′(x)<0,
当x>![]() 时,f′(x)>0,
时,f′(x)>0,
∴f(x)在[-![]() ,
,![]() )上是减函数,在[
)上是减函数,在[![]() ,+∞)上是增函数.
,+∞)上是增函数.
从而f(x)min=f(![]() )=
)=![]() ,
,
|C2M|min=![]()
![]() .
.
若r≥![]()
![]() ,
,
由y=![]() +1在[-
+1在[-![]() ,+∞)上是增函数可知曲线C1与圆C2有公共点,
,+∞)上是增函数可知曲线C1与圆C2有公共点,
则它们的距离为0,这与已知条件矛盾.
故r<![]()
![]() ,
,
即曲线C1在圆C2外,设N是圆C2上任一点.
设线段C2M与圆C2交于点Q,
则|C2M|≤|MN|+|C2N|,
即|QM|≤|MN|.
当N与Q重合时,|MN|=|QM|,
∴|MN|min=|QM|min=|C2M|min-r=![]() ,
,
r=![]()
![]() -
-![]() =
=![]() .
.

练习册系列答案
相关题目