题目内容
4.当x>-3时,不等式a≤x+$\frac{2}{x+3}$恒成立,则a的取值范围是2$\sqrt{2}$-3.分析 a≤x+$\frac{2}{x+3}$恒成立,只需求出x+$\frac{2}{x+3}$的最小值,令f(x)=x+$\frac{2}{x+3}$,得出f(x)=x+3+$\frac{2}{x+3}$-3≥2$\sqrt{2}$-3,
得出a的范围.
解答 解:a≤x+$\frac{2}{x+3}$恒成立,
令f(x)=x+$\frac{2}{x+3}$,
∵x>-3,
∴f(x)=x+3+$\frac{2}{x+3}$-3≥2$\sqrt{2}$-3,
∴a≤2$\sqrt{2}$-3.
点评 考查了恒成立问题和均值定理.属于基础题型,应熟练掌握.

练习册系列答案
相关题目
14.数列{an}共有六项,其中四项是1,其余两项各不相同,则满足上述条件的数列{an}共有( )
| A. | 30个 | B. | 31个 | C. | 60个 | D. | 61个 |
19.终边在第二象限的角的集合可以表示为( )
| A. | {α|90°<α<180°} | |
| B. | {α|90°+k•180°<α<180°+k•180°,k∈Z} | |
| C. | {α|-270°+k•180°<α<-180°+k•180°,k∈Z} | |
| D. | {α|-270°+k•360°<α<-180°+k•360°,k∈Z} |
10.已知两条直线m,n和平面α,那么下列命题中的真命题为( )
| A. | 若m∥n,n?α,则m∥α | B. | 若m⊥n,n?α,则m⊥α | ||
| C. | 若m∥n,n?α,m?α,则m∥α | D. | 若m⊥n,n?α,m?α,则m⊥α |
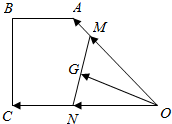 如图所示,已知直角梯形ABCO中,∠ABC=∠BCO=90°,AB=1,BC=$\sqrt{3}$,OA=OC=2,设$\overrightarrow{OM}$=m$\overrightarrow{OA}$,$\overrightarrow{ON}$=n$\overrightarrow{OC}$(其中0<m,n<1),G为线段MN的中点.
如图所示,已知直角梯形ABCO中,∠ABC=∠BCO=90°,AB=1,BC=$\sqrt{3}$,OA=OC=2,设$\overrightarrow{OM}$=m$\overrightarrow{OA}$,$\overrightarrow{ON}$=n$\overrightarrow{OC}$(其中0<m,n<1),G为线段MN的中点.