题目内容
如图1-1-2,圆O1与圆O2的半径都是1,|O1O2|=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得PM=
图1-1-2
思路分析:本题利用数形结合思想、勾股定理、两点间距离公式等相关知识点,及分析推理、计算化简技能、技巧等,是一道很综合的题目.由题意建立坐标系,写出相关点的坐标,由几何关系式PM=![]() PN,即(PM)2=2(PN)2,结合图形由勾股定理转化为PO12-1=2(PO22-1),设P(x,y),由距离公式写出代数关系式,化简整理可得.
PN,即(PM)2=2(PN)2,结合图形由勾股定理转化为PO12-1=2(PO22-1),设P(x,y),由距离公式写出代数关系式,化简整理可得.

图1-1-3
解:如图1-1-3,以直线O1O2为x轴,线段O1O2的垂直平分线为y轴,建立平面直角坐标系,则两圆心的坐标分别为O1(-2,0),O2(2,0).
设P(x,y),则PM2=PO12-MO12=(x+2)2+y2-1.
同理,PN2=(x-2)2+y2-1.
∵PM=![]() PN,∴(x+2)2+y2-1=2[(x-2)2+y2-1],
PN,∴(x+2)2+y2-1=2[(x-2)2+y2-1],
即x2-12x+y2+3=0,即(x-6)2+y2=33,这就是动点P的轨迹方程.
深化升华 在求轨迹方程时,首先能够建立一个适当的坐标系.同一几何图形的方程在不同坐标系中具有不同的形式.选择适当的坐标系可以使表示图形的方程具有更方便的形式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
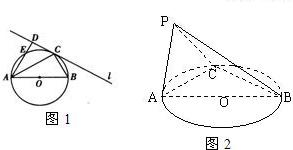 如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E.
如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E. 如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E.
如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E. 则圆O的半径R=_____ _.
则圆O的半径R=_____ _. 则圆O的半径R=_____ _.
则圆O的半径R=_____ _.