题目内容
设数列{an}的前n项积为Tn,Tn=1-an;数列{bn}的前n项和为Sn,Sn=1-bn,
(Ⅰ)设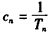 ,
,
①证明数列{cn}成等差数列;
②求数列{an}的通项公式;
(Ⅱ)若Tn(nbn+n-2)≤kn对n∈N*恒成立,求实数k的取值范围.
(Ⅰ)设
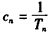 ,
,①证明数列{cn}成等差数列;
②求数列{an}的通项公式;
(Ⅱ)若Tn(nbn+n-2)≤kn对n∈N*恒成立,求实数k的取值范围.
解:(Ⅰ)①由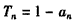 ,得
,得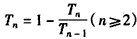 ,
,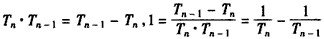 ,
,
即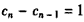 ,
,
又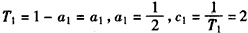 ,
,
所以,数列{cn}是以2为首项,1为公差的等差数列。
②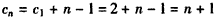 ,
,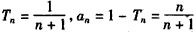 。
。
(Ⅱ)因为Sn=1-bn,S1=1-b1=b1,
所以b1=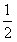 ,Sn-1=1-bn-1(n≥2),Sn-Sn-1=bn-1-bn,2bn=bn-1(n≥2),
,Sn-1=1-bn-1(n≥2),Sn-Sn-1=bn-1-bn,2bn=bn-1(n≥2),
所以数列{bn}是以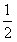 为首项,
为首项,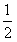 为公比的等比数列,
为公比的等比数列,
所以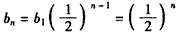 。
。
因为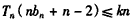 对n∈N*恒成立,
对n∈N*恒成立,
所以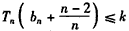 对n∈N*恒成立,
对n∈N*恒成立,
即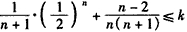 对n∈N*恒成立,
对n∈N*恒成立,
设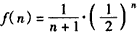 ,
,
则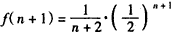 ,
,
因为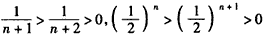 ,
,
所以f(n)>f(n+1),
所以,当n∈N*时,f(n)单调递减,
设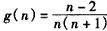 ,则
,则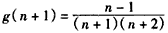 ,
, 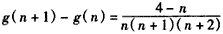 ,
,
所以,当1≤n<4时,g(n)单调递增;g(4)=g(5);当n≥5时,g(n)单调递减;
设L(n)=f(n)+g(n),则 L(1)<L(2)<L(3),L(3)>L(4)>L(5)>L(6)>……,
所以L(3)最大,且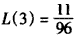 ,
,
所以,实数k的取值范围为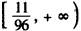 。
。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目