题目内容
如果函数f(x)=ax5-bx3+c(a≠0)在x=±1时有极值,极大值为4,极小值为0,试求a,b,c的值.
思路分析:可通过求导确定可疑点,注意利用已知极值点x=±1所确定的相关等式,在判断y′的符号时,必须对a进行分类讨论.
解:y′=5ax4-3bx2,令y′=0,即5ax4-3bx2=0,x2(5ax2-3b)=0,
∵x=±1是极值点,
∴5a(±1)2-3b=0.
又x2>0,∴可疑点为x=0,±1.
若a>0,y′=5ax2(x2-1).
当x变化时,y′与y的变化情况如下表:
X | (-∞,1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
y′ | + | 0 | - | 0 | - | 0 | + |
Y | ↗? | 极大值 | ?↘ | 无极值 | ?↘ | 极小值 | ↗? |
∴当x=-1时,f(x)有极大值;
当x=1时,f(x)有极小值.
∴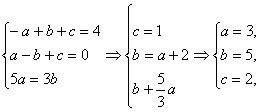
若a<0,同理可得a=-3,b=-5,c=2.
方法归纳 从逆向思维出发,运用待定系数法,实现由已知向未知的转化,转化过程中通过列表形象直观地解决待定系数问题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
如果函数f(x)=
是奇函数,那么a=( )
| a•2x+a-2 |
| 2x+1 |
| A、1 | B、2 | C、-1 | D、-2 |