题目内容
已知不等式ax2+bx+c＞0的解集为{x|α＜x＜β,β＞α＞0},求不等式cx2+bx+a＜0的解集.思路分析：欲求不等式cx2+bx+a＜0的解集,则要确定c的正负,以及cx2+bx+a=0的两根和大小.
解:由题意(不等式解集的“形”)可知a＜0,∴x2+
x+
＜0.
由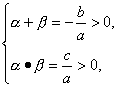
结合a＜0,可得c＜0,b＞0.
∴cx2+bx+a＜0可化为x2+
＞0.
∵
=
·
=-
=-(
),
=
,
∴(x-
)(x-
)＞0.所求不等式的解集为{x|x＞
或x＜
}.
温馨提示
解这类题目,二次项系数的符号为正至关重要.另外,一元二次不等式的解与一元二次方程的根有密切关系.因此常常用到韦达定理.
练习册系列答案
相关题目