题目内容
设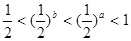
，那么
A． | B． | C． | D． |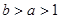
B
解析试题分析：根据指数函数底数小于1，那么可知函数在定义域内递减可知，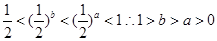
，故可知答案为B.
考点：指数函数的性质
点评：主要是考查了指数函数的单调性的运用，属于基础题。
练习册系列答案
阅读快车系列答案
相关题目
已知a是函数
的零点，
a，则
的值满足( )
| A．＝0 | B．＞0 |
| C．＜0 | D．的符号不确定 |
为了得到函数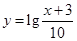
的图像，只需把函数
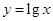的图像上所有的点（ ）
| A．向左平移3个单位长度，再向上平移1个单位长度 |
| B．向右平移3个单位长度，再向上平移1个单位长度 |
| C．向左平移3个单位长度，再向下平移1个单位长度 |
| D．向右平移3个单位长度，再向下平移1个单位长度 |
设集合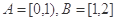
，函数
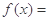
且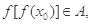
则
的取值范围是 ( )
A．( ) | B．[0， ] | C．( ) | D．( ) |
设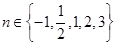
，则使得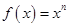
为奇函数，且在
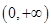上单调递减的
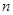的个数为
| A．1 | B．2 | C．3 | D．4 |
若函数
，则
的值是（ ）
| A．9 | B． | C．-9 | D． |
，形状为直角三角形的铁架框，有下列四种长度的铁管供选择，较经济（够用，又耗材最少）的是 
定义运算
，函数
图像的顶点是
，且
成等差数列，则
( )
| A．0 | B．－14 | C．－9 | D．－3 |
如果
，那么
的最小值是（ ）
| A．4 | B． | C．9 | D．18 |