Question

已知：f（x）=cosx，
（1）在x∈[0，2π]内画出f（x）的图象；
（2）写出f（x）的单调递减区间；
（3）求f（x）的最小值及达到最小值时x的集合．

Answer 1

分析：（1）利用五点作图法作出函数f（x）=cosx在x∈[0，2π]内的图象；
（2）直接由图象得到函数的减区间；
（3）由图象得到函数的最小值，借助于函数的周期性得到函数达到最小值时的x的集合．

解答：解：（1）列表：

描点并用平滑曲线连结，如图：

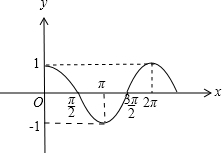
（2）单调递减区间为：[2kπ，2kπ+π]，k∈Z；
（3）最小值为-1，此时x的集合为{x|x=2kπ+π，k∈Z}．

点评：本题考查了余弦函数的图象，考查了余弦函数的最值及单调性，是中低档题．