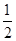题目内容
《莱因德纸草书》是世界上最古老的数学著作之一．书中有一道这样的题目：把100个面包分给5个人，使每人所得成等差数列，且使较大的三份之和的
是较小的两份之和，问最小1份为( )
A． | B． | C． | D． |
A
解析试题分析：设最小1份为
，公差为
则有
解得
.
考点：等差数列求和
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
等差数列
,
的前
项和分别为
,
,若
,则
=（ ）
A． | B． | C． | D． |
等差数列{an}满足a42＋a72＋2a4a7＝9，则其前10项之和为( )
| A．－9 | B．－15 | C．15 | D．±15 |
图像上存在不同的三点到原点的距离构成等比数列，则以下
设等差数列
的前n项和为
，若
，则必定有
A． | B． |
C． | D． |
等比数列
的前
项和为
，且4
，2
，
成等差数列。若=1，则
=（ ）
| A．7 | B．8 | C．15 | D．16 |
若
为等差数列，
数列
满足
则
（ ）
| A．56 | B．57 | C．72 | D．73 |
已知数列
满足
，
，则
A． | B． | C． | D． |
