题目内容
已知结论:“在正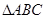 中,
中,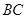 中点为
中点为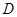 ,若
,若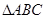 内一点
内一点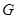 到各边的距离都相等,则
到各边的距离都相等,则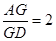 ”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体
”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体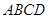 中,若
中,若 的中心为
的中心为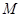 ,四面体内部一点
,四面体内部一点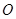 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则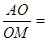 ( ▲ )
( ▲ )
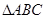 中,
中,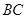 中点为
中点为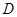 ,若
,若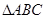 内一点
内一点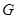 到各边的距离都相等,则
到各边的距离都相等,则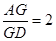 ”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体
”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体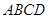 中,若
中,若 的中心为
的中心为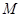 ,四面体内部一点
,四面体内部一点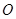 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则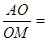 ( ▲ )
( ▲ )| A.1 | B.2 | C.3 | D.4 |
C
解:设正四面体ABCD边长为1,易求得AM= 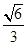 ,又O到四面体各面的距离都相等,
,又O到四面体各面的距离都相等,
所以O为四面体的内切球的球心,设内切球半径为r,则有r="3V" /S表 ,可求得r即OM=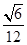 ,所以AO="AM-OM="
,所以AO="AM-OM=" 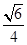 ,所以AO OM =3 故答案为:3
,所以AO OM =3 故答案为:3
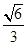 ,又O到四面体各面的距离都相等,
,又O到四面体各面的距离都相等,所以O为四面体的内切球的球心,设内切球半径为r,则有r="3V" /S表 ,可求得r即OM=
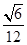 ,所以AO="AM-OM="
,所以AO="AM-OM=" 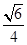 ,所以AO OM =3 故答案为:3
,所以AO OM =3 故答案为:3
练习册系列答案
相关题目
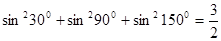

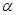 都成立的一般性命题并证明。
都成立的一般性命题并证明。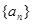 的前
的前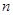 项和
项和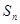 满足
满足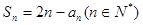 .
.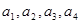 的值;
的值; ,经计算得
,经计算得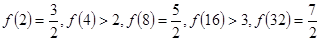 观察上式结果,可推测出一般结论
观察上式结果,可推测出一般结论 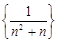 依次按第一个括号一个数,第二个括号两
依次按第一个括号一个数,第二个括号两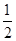 ),(
),(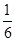 ,
,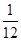 ),(
),(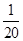 ,
, 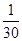 ,
,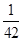 ),(
),(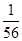 ,
,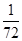 ,
,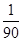 ,
,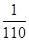 ),
), 是三角函数,所以
是三角函数,所以




 均为正实
均为正实 .
.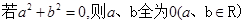 ”,其反设正确的是( )
”,其反设正确的是( )



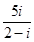 = ( )
= ( )