题目内容
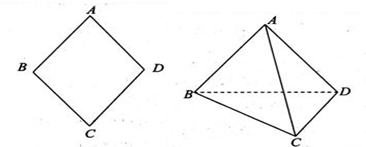
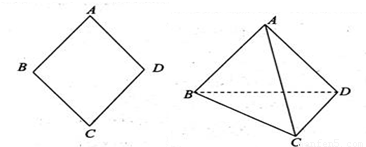
如图所示,已知菱形ABCD的边长为2,AC∩BD=O.∠DAB=60°,将菱形ABCD沿对角线AC折起,得到三棱锥D-ABC.
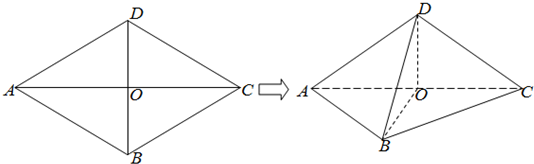
(1)求证:平面BOD⊥平面ABC;
(2)若三棱锥D-ABC的体积为
,求BD的长.

(1)求证:平面BOD⊥平面ABC;
(2)若三棱锥D-ABC的体积为
| 1 | 2 |
分析:(1)由ABCD是菱形,知DO⊥AC,BO⊥AC,由此能够证明面ABC⊥面BOD.
(2)由VD-ABC=
AC•S△BOD=
×2
•S△BOD=
×2
×
×1×1•sin∠BOD=
,能够推导出∠BOD=
或
,由此及彼能求出BD的长.
(2)由VD-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
解答:解:(1)∵ABCD是菱形,∴DO⊥AC,(2分)
BO⊥AC,(4分)
BO∩DO=0,BO、DO?面BOD,AC?面BOD,
∴AC⊥面BOD,(5分)
∵AC?面ABC,∴面ABC⊥面BOD.(6分)
(2)VD-ABC=
AC•S△BOD=
×2
•S△BOD
=
×2
×
×1×1•sin∠BOD=
,
sin∠BOD=
⇒∠BOD=
或
(8分)
①若∠BOD=
,BD2=BO2+DO2-2•BO•DO•cos
=1+1-1=1,所以BD=1(10分)
②若∠BOD=
,BD2=BO2+DO2-2•BO•DO•cos
=1+1+1=3,所以BD=
综上,BD=1或
.(12分)
BO⊥AC,(4分)
BO∩DO=0,BO、DO?面BOD,AC?面BOD,
∴AC⊥面BOD,(5分)
∵AC?面ABC,∴面ABC⊥面BOD.(6分)
(2)VD-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
=
| 1 |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
sin∠BOD=
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
①若∠BOD=
| π |
| 3 |
| π |
| 3 |
②若∠BOD=
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
综上,BD=1或
| 3 |
点评:本题考查平面与平面垂直的证明,考查满足条件的线段长的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
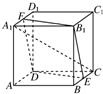 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.
如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点. 如图所示,已知点P为菱形ABCD外一点,且PA⊥面ABCD,PA=AD=AC,点F为PC中点,则二面角CBFD的正切值为( )
如图所示,已知点P为菱形ABCD外一点,且PA⊥面ABCD,PA=AD=AC,点F为PC中点,则二面角CBFD的正切值为( )