题目内容
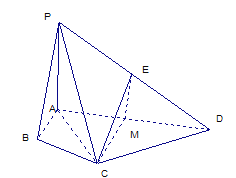
【题目】如图，在四棱锥
中， 
， 
平面
. 
为
的中点， 
.
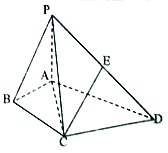
(1)求证： 
平面
；
(2)求三棱锥
的体积.
【答案】（1）见解析；（2）
【解析】试题分析：1）法一： 取AD得中点M，连接EM,CM.则EM//PA
因为
所以，EM∥平面PAB （2分）
在Rt△ACD中， 
所以， 
而
,所以MC//AB （3分）
因为
所以， 
平面PAB （4分）
又因为
所以，平面EMC∥平面PAB
因为EC
平面EMC，∴EC∥平面PAB （6分）
法二： 延长DC,AB,交于N点，连接PN.
因为
所以C为ND的中点. （3分）
因为E为PD的中点，所以，EC//PN
因为
∴EC∥平面PAB （6分）
2）法一：由已知条件有;AC=2AB=2,AD=2AC=4,CD=
.（7分）
因为PA⊥平面ABCD，所以PA⊥CD （8分）
又因为CD⊥AC，AC∩PA=A，所以CD⊥平面PAC ..（10分）
因为E是PD的中点，所以点E平面PAC的距离h=
，
所以，四面体PACE的体积
（12分）
法二：由已知条件有;AC=2AB=2,AD=2AC=4,CD=
因为PA⊥平面ABCD，所以
.（10分）
因为E是PD的中点，所以，四面体PACE的体积
..（12分）
练习册系列答案
相关题目
【题目】某种产品的广告费支出
(百万元)与销售额
(百万元)之间有如下对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 50 | 60 | 70 |
如果
与
之间具有线性相关关系.
（1）作出这些数据的散点图；
（2）求这些数据的线性回归方程
;
（3）预测当广告费支出为9百万元时的销售额。 ( 参考数据： 
)
