题目内容
已知定义在[-1,1]上的奇函数f(x),当x∈(0,1]时,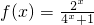 .
.
(1)求函数f(x)在[-1,1]上的解析式;
(2)判断f(x)在(0,1]上的单调性,并证明;
(3)要使方程f(x)=x+b在[-1,1]上恒有实数解,求实数b的取值范围.
解:(1)设x∈[-1,0),则-x∈(0,1]
∵当x∈(0,1]时,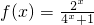
∴
∵f(x)是奇函数
∴f(x)=-f(-x)=
∵f(0)=0
∴函数f(x)在[-1,1]上的解析式为f(x)= ;
;
(2)f(x)在(0,1]上单调递减,证明如下:
∵当x∈(0,1]时,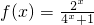 ,
,
∴
∵x∈(0,1],∴f′(x)<0
∴f(x)在(0,1]上单调递减;
(3)记g(x)=f(x)-x,则g(x)为(0,1]上的单调递减函数.
∴g(x)∈[g(1),g(0))?g(x)∈[- ,
, ).
).
∵g(x)在[-1,1]上为奇函数,∴当x∈[-1,0)时g(x)∈(- ,
, ].
].
又g(0)=0,
∴g(x)∈[- ,
, ],即b∈[-
],即b∈[- ,
, ].
].
分析:(1)设x∈[-1,0),则-x∈(0,1],利用当x∈(0,1]时,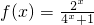 ,函数为奇函数,可求函数的解析式;
,函数为奇函数,可求函数的解析式;
(2)利用导数,判断导数小于0,即可求得函数的单调性;
(3)将b表示为x的函数,利用单调性求f(x)-x在[-1,1]上值域,即可求得实数b的取值范围
点评:本题考查单调性与奇偶性,考查函数的解析式,考查单调性的证明,考查函数的值域,属于中档题.
∵当x∈(0,1]时,
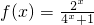
∴

∵f(x)是奇函数
∴f(x)=-f(-x)=

∵f(0)=0
∴函数f(x)在[-1,1]上的解析式为f(x)=
 ;
;(2)f(x)在(0,1]上单调递减,证明如下:
∵当x∈(0,1]时,
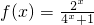 ,
,∴

∵x∈(0,1],∴f′(x)<0
∴f(x)在(0,1]上单调递减;
(3)记g(x)=f(x)-x,则g(x)为(0,1]上的单调递减函数.
∴g(x)∈[g(1),g(0))?g(x)∈[-
 ,
, ).
).∵g(x)在[-1,1]上为奇函数,∴当x∈[-1,0)时g(x)∈(-
 ,
, ].
].又g(0)=0,
∴g(x)∈[-
 ,
, ],即b∈[-
],即b∈[- ,
, ].
].分析:(1)设x∈[-1,0),则-x∈(0,1],利用当x∈(0,1]时,
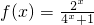 ,函数为奇函数,可求函数的解析式;
,函数为奇函数,可求函数的解析式;(2)利用导数,判断导数小于0,即可求得函数的单调性;
(3)将b表示为x的函数,利用单调性求f(x)-x在[-1,1]上值域,即可求得实数b的取值范围
点评:本题考查单调性与奇偶性,考查函数的解析式,考查单调性的证明,考查函数的值域,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目