题目内容
下列命题中,真命题的个数是( )
①a∥b,a,c异面,则b、c异面 ②a,b共面,b、c异面,则a、c异面
③a,b异面,a、c共面,则b、c异面 ④a,b异面,b、c不相交,则a、c不相交.
①a∥b,a,c异面,则b、c异面 ②a,b共面,b、c异面,则a、c异面
③a,b异面,a、c共面,则b、c异面 ④a,b异面,b、c不相交,则a、c不相交.
分析:根据两条直线的位置关系,进行判断,或举出反例进行求解即得.
解答:解:①a∥b,a,c异面,则b、c异面也可以相交,故①错误;
②a,b共面,b、c异面,则a、c异面也可以相交,故②错误;
③a,b异面,a、c共面,则b、c异面也可以相交,故③不正确;
④a,b异面,b、c不相交,则a、c也有可能相交,故④错误;
故选A.
②a,b共面,b、c异面,则a、c异面也可以相交,故②错误;
③a,b异面,a、c共面,则b、c异面也可以相交,故③不正确;
④a,b异面,b、c不相交,则a、c也有可能相交,故④错误;
故选A.
点评:此题主要考查命题的真假判断与应用,利用举反例法求解,会比较简单,是一道基础题.

练习册系列答案
相关题目
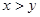 ,则
,则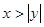 ”的逆命题
”的逆命题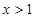 ,则
,则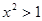 ”的否命题
”的否命题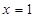 ,则
,则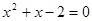 ”的否命题
”的否命题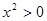 ,则
,则