Question

20.已知函数f(x)=x²+x-1，α、β是方程f(x)=0的两个根(α＞β)，f′(x)是f(x)的导数.设a₁=1，a_n+1=a_n-(n=1，2，…).

(1)求α、β的值；

(2)已知对任意的正整数n有a_n＞α，记b_n=ln(n=1，2，…).求数列{b_n}的前n项和S_n.

Answer 1

解：（1）由x²+x-1=0解得方程的两根为x_1,2=

又∵α、β是方程的两个根，且α＞β,

∴

(2) ∵∴a_n+1=

∵a_n＞α＞β(n=1,2,3,…)，且a₁=1,

∴b₁=1n

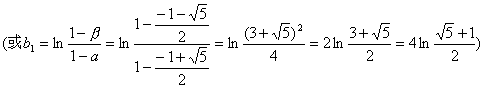
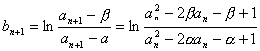
即{b_n}是以b₁为首项,以2为公比的等比数列.

故数列{b_n}前n项之和为

S_n=