题目内容

某工厂生产甲、乙两种产品，其产量分别为45个和55个，所用原料为A、B两种规格的金属板，每张面积分别是2m2和3m2，用A种规格金属板可造甲种产品3个和乙种产品5个，用B种规格金属板可造甲、乙两种产品各6个，问A、B两种规格的金属板各取多少张才能完成计划并使总的用料面积最省？

   

思路分析：本题属于给定一项任务，问怎样统筹安排才能使完成这项任务的人力、物力资源最小的题型.解决这种问题的方法是：根据题意列出不等式组（约束条件），确定目标函数；然后由约束条件找到可行域；最后利用目标函数的平移，在可行域内求出目标函数的最小值的点，从而求出符合题意的解.

    解：设A、B两种金属板各取x张、y张，用料面积为Z，则约束条件是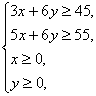

    目标函数是Z=2x+3y，

    作出以上不等式组所表示的平面区域，即可行域，如下图所示Z=2x+3y变为y=-x+，得斜率为-，在y轴上截距为且随Z变化的一族平行直线，

  

当直线Z=2x+3y过平行域上点M时，截距最小，Z最小.解方程得M点坐标为（5，5）.

    此时Zmin＝2×5+3×5＝25（m2）.

     答：两种金属板各取5张时，用料面积最省.


练习册系列答案
相关题目
某工厂生产甲、乙两种产品，甲产品的一等品率为80%，二等品率为20%；乙产品的一等品率为90%，二等品率为10%．生产1件甲产品，若是一等品则获得利润4万元，若是二等品则亏损1万元；生产1件乙产品，若是一等品则获得利润6万元，若是二等品则亏损2万元．设生产各种产品相互独立．
（1）记X（单位：万元）为生产1件甲产品和1件乙产品可获得的总利润，求X的分布列；
（2）求生产4件甲产品所获得的利润不少于10万元的概率．
18、某工厂生产甲、乙两种产品，每种产品都是经过第一道和第二道工序加工而成，两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级，对每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品
（1）已知甲、乙两种产品每一道工序的加工结果为A级的概率如表一所示，分别求生产的甲、乙产品为一等品的概率P甲、P乙；
（2）已知一件产品的利润如表二所示，用ξ、η分别表示一件甲、乙产品的利润，在（1）的条件下，分别求甲、乙两种产品利润的分布列及数学期望．
某工厂生产甲、乙两种产品．已知生产一吨甲产品、一吨乙产品所需要的煤、电以及产值如表所示；
用煤（吨） 用电（千瓦） 产值（万元）
生产一吨甲种产品 7 2 8
生产一吨乙种产品 3 5 11
又知道国家每天分配给该厂的煤和电力有限制，每天供煤至多56吨，供电至多45千瓦．问该厂如何安排生产，才能使该厂日产值最大？最大的产值是多少？
某工厂生产甲、乙两种产品，这两种产品每千克的产值分别为600元和400元，已知每生产1千克甲产品需要A种原料4千克，B种原料2千克；每生产1千克乙产品需要A种原料2千克，B种原料3千克．但该厂现有A种原料100千克，B种原料120千克．问如何安排生产可以取得最大产值，并求出最大产值．
某工厂生产甲、乙两种产品，已知生产每吨甲产品所需电力4千瓦时、劳力6个，获得利润5百元；生产每吨乙产品所需电力5千瓦时、劳力4个，获得利润4百元；每天资源限额（最大供应量）分别为电力202千瓦时、劳动力240个．
问：每天生产甲、乙两种产品各多少吨，获得利润总额最大？最大利润是多少？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网