题目内容
已知定义在R上的单调函数f(x),存在实数x0,使得对于任意实数x1,x2,总有f(x0x1+x0x2)=f(x0)+f(x1)+f(x2)恒成立.(Ⅰ)求x0的值;
(Ⅱ )若f(x0)=1,且对任意正整数n,有an=![]() ,bn=f
,bn=f![]() +1,记Sn=a1a2+a2a3+…+anan+1,
+1,记Sn=a1a2+a2a3+…+anan+1,
Tn=b1b2+b2b3+…+bnbn+1,比较![]() Sn与Tn的大小关系,并给出证明;
Sn与Tn的大小关系,并给出证明;
(Ⅲ )若不等式an+1+an+2+…+a2n>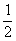 对任意不小于2的正整数n都成立,求x的取值范围.
对任意不小于2的正整数n都成立,求x的取值范围.
解:(Ⅰ)令x1=x2=0,得f(0)=f(x0)+2f(0).
∴f(x0)=-f(0). ①
令x1=1,x2=0,得f(x0)=f(x0)+f(1)+f(0),
∴f(1)=-f(0). ②
由①,②得 f(x0)=f(1).
∵f(x)为单调函数,∴x0=1.
(Ⅱ)由(Ⅰ)得f(x1+x2)=f(x1)+f(x2)+f(1)
=f(x1)+f(x2)+1,
∵f(n+1)=f(n)+f(1)+1=f(n)+2,f(1)=1,∴f(n)=2n-1. (n∈Z*)
∴an=![]() .
.
又∵f(1)=f(![]() +
+![]() )=f(
)=f(![]() )+f(
)+f(![]() )=f(1)∴f(
)=f(1)∴f(![]() )=0,b1=f(
)=0,b1=f(![]() )+1.
)+1.
又∵f(![]() )=f(
)=f(![]() )=f(
)=f(![]() )+f(
)+f(![]() )=f(1)=2f(
)=f(1)=2f(![]() )+1,
)+1,
∴2bn+1=2f(![]() )+2=f(
)+2=f(![]() )+1=bn.
)+1=bn.
∴bn=(![]() )n-1.
)n-1.
∴Sn=![]()
=![]()
=![]() .
.
Tn=(![]() )0(
)0(![]() )1+(
)1+(![]() )1(
)1(![]() )2+…+(
)2+…+(![]() )n-1(
)n-1(![]() )n
)n
=![]() +(
+(![]() )3+…+(
)3+…+(![]() )2n+1
)2n+1
=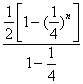
=![]()
![]() .
.
∴![]() Sn-Tn=
Sn-Tn=![]() (1-
(1-![]() )-
)-![]()
![]()
∵4n=(3+1)n=![]() 3n+
3n+![]() 3n-1+…+
3n-1+…+![]() 3+
3+![]() ≥3n+1>2n+1,
≥3n+1>2n+1,
∴![]() Sn-Tn=
Sn-Tn=![]() (
(![]() )<0.∴
)<0.∴![]() Sn<Tn.
Sn<Tn.
(Ⅲ)令F(n)=an+1+an+2+…a2n,
则F(n+1)-F(n)=a2n+1+a2n+2-an-1
=![]() >0.
>0.
∴当n≤2,n∈N时,
F(n)>F(n-1)>…>F(2)=a3+a4=![]() .
.
∴![]() >
>![]()
 .
.
即![]() (x+1)-
(x+1)-![]() (9x2-1)<2.
(9x2-1)<2.
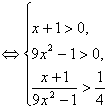 .解得
.解得![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案