题目内容
如图，AD=2，AC=4，BC=6，∠B=36°，∠D=117°，△ABC∽△DAC．（1）求AB的长；
（2）求CD的长；
（3）求∠BAD的大小．
分析：（1）（2）根据相似三角形的性质求出∠DAC和∠BAC的度数，找出对应边．然后根据已知边的长求出边AB和CD的长；
（3）然后根据相似三角形对应角相等，求出∠BAD的大小．
（3）然后根据相似三角形对应角相等，求出∠BAD的大小．
解答：解：△ABC∽△DAC
∴∠DAC=∠B=36°，∠BAC=∠D=117°
=
=
，
又AD=2，AC=4，BC=6，
∴AB=3，CD=
．
∠BAD=∠DAC+∠BAC=36°+117°=153°．
答：（1）AB的长是3；（2）CD的长是
；（3）∠BAD是153°．
∴∠DAC=∠B=36°，∠BAC=∠D=117°
| AB |
| AD |
| AC |
| CD |
| BC |
| AC |
又AD=2，AC=4，BC=6，
∴AB=3，CD=
| 8 |
| 3 |
∠BAD=∠DAC+∠BAC=36°+117°=153°．
答：（1）AB的长是3；（2）CD的长是
| 8 |
| 3 |
点评：本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力．
练习册系列答案
相关题目
如图，圆O上一点C在直径AB上的射影为D．AD=2，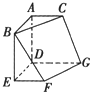
已知多面体ABC-DEFG中（如图），AB、AC、AD两两互相垂直，平面ABC∥平面DEFG，平面BEF∥平面ADGC，AB=AD=DG=2，AC=EF=1，则这个多面体的体积为（ ）
（2011•渭南三模）选做题（请考生在以下三个小题中任选一题作答，如果多做，则按所做的第一题评阅记分）