题目内容
设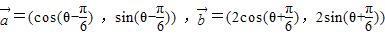 .
.(1)若向量
 与向量
与向量 的夹角为锐角,求实数t的取值范围;
的夹角为锐角,求实数t的取值范围;(2)当t在区间(0,1]上变化时,求向量
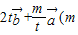 为常数,且m>0)的模的最小值.
为常数,且m>0)的模的最小值.
【答案】分析:(1)由已知可求 ,
, ,
, ,由夹角为锐角,代入
,由夹角为锐角,代入 =2t|
=2t| |
| >0,解不等式可求t的范围,舍去
>0,解不等式可求t的范围,舍去 =
= 中t即可
中t即可
(2)由 =
= =
= ,结合y=
,结合y= ,t∈(0,1]的单调性可求y的最小值
,t∈(0,1]的单调性可求y的最小值
解答:解:(1)由题设易得 ,|
,| |=2,
|=2, =
= =1
=1
∴ =
= =2t|
=2t| |2
|2 +7t
+7t >0
>0
整理可得,2t2+15t+7>0
∴ 或 t<-7
或 t<-7
又当 与
与 共线时,不满足题意.
共线时,不满足题意.
令 =
=
则 ∴
∴
∴ 或 t<-7,且t
或 t<-7,且t (6分)
(6分)
(2)∵ =
=
=
令y= t∈(0,1]
t∈(0,1]
∵y= ≥8m+4m=12m
≥8m+4m=12m
当且仅当
于是①当 即 0<m≤4时
即 0<m≤4时
当且仅当 时,ymin=12m.从而
时,ymin=12m.从而
②当 即m>4时
即m>4时
可证 在(0,1]为减函数
在(0,1]为减函数
从而当t=1时,ymin=m2+4m+16
∴ (6分)
(6分)
点评:本题主要考查了向量的数量积的性质的综合应用,注意:向量 的夹角θ为锐角时,并不等价于
的夹角θ为锐角时,并不等价于 ,一定要把向量同向的情况去掉,及函数的单调性在求解函数最值中的应用.
,一定要把向量同向的情况去掉,及函数的单调性在求解函数最值中的应用.
 ,
, ,
, ,由夹角为锐角,代入
,由夹角为锐角,代入 =2t|
=2t| |
| >0,解不等式可求t的范围,舍去
>0,解不等式可求t的范围,舍去 =
= 中t即可
中t即可(2)由
 =
= =
= ,结合y=
,结合y= ,t∈(0,1]的单调性可求y的最小值
,t∈(0,1]的单调性可求y的最小值解答:解:(1)由题设易得
 ,|
,| |=2,
|=2, =
= =1
=1 ∴
 =
= =2t|
=2t| |2
|2 +7t
+7t >0
>0整理可得,2t2+15t+7>0
∴
 或 t<-7
或 t<-7又当
 与
与 共线时,不满足题意.
共线时,不满足题意.令
 =
=
则
 ∴
∴
∴
 或 t<-7,且t
或 t<-7,且t (6分)
(6分)(2)∵
 =
=
=

令y=
 t∈(0,1]
t∈(0,1]∵y=
 ≥8m+4m=12m
≥8m+4m=12m当且仅当

于是①当
 即 0<m≤4时
即 0<m≤4时当且仅当
 时,ymin=12m.从而
时,ymin=12m.从而
②当
 即m>4时
即m>4时可证
 在(0,1]为减函数
在(0,1]为减函数从而当t=1时,ymin=m2+4m+16
∴
 (6分)
(6分)点评:本题主要考查了向量的数量积的性质的综合应用,注意:向量
 的夹角θ为锐角时,并不等价于
的夹角θ为锐角时,并不等价于 ,一定要把向量同向的情况去掉,及函数的单调性在求解函数最值中的应用.
,一定要把向量同向的情况去掉,及函数的单调性在求解函数最值中的应用. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,设Ox,Oy是平面内相交成60°角的两条数轴,
如图,设Ox,Oy是平面内相交成60°角的两条数轴,